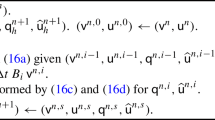A Neumann series of Bessel functions representation for solutions of Sturm–Liouville equations

Abstract

A Neumann series of Bessel functions (NSBF) representation for solutions of Sturm–Liouville equations and for their derivatives is obtained. The representation possesses an attractive feature for applications: for all real values of the spectral parameter $\omega$ the estimate of the difference between the exact solution and the approximate one (the truncated NSBF) depends on N (the truncation parameter) and the coefficients of the equation and does not depend on $\omega$. A similar result is valid when $\omega \in {\mathbb {C}}$ belongs to a strip $\left| \hbox {Im }\omega \right| <C$. This feature makes the NSBF representation especially useful for applications requiring computation of solutions for large intervals of $\omega$. Error and decay rate estimates are obtained. An algorithm for solving initial value, boundary value or spectral problems for the Sturm–Liouville equation is developed and illustrated on a test problem.

Error and decay rate estimates

In this appendix some estimates for the functions $\varepsilon _{N}$ and $\varepsilon _{1,N}$ from Theorems 3.1 and 3.2 are presented. Also decay rate estimates and bounds near $x=0$ for the coefficients $\beta _{n}$ and $\gamma _{n}$ are obtained in dependence on the smoothness of the potential Q. The estimates are from [13] with some additional improvements obtained using ideas from [15].

It is well known (see, e.g., [19,20,21,22]) that the solutions $c(\omega ,x)$ and $s(\omega ,x)$ of (2.3) satisfying the initial conditions (3.1) can be represented as

$$\begin{aligned} c(\omega ,x)=\cos \omega x+\int _{-x}^{x}K(x,t)\cos \omega t\,dt \end{aligned}$$

and

$$\begin{aligned} s(\omega ,x)=\sin \omega x+\int _{-x}^{x}K(x,t)\sin \omega t\,dt, \end{aligned}$$

i.e., as images of the functions $\cos \omega t$ and $\sin \omega t$ under the action of the so-called transmutation operator T. This operator is defined on an arbitrary integrable function by the rule

$$\begin{aligned} Tu(x)=u(x)+\int _{-x}^{x}K(x,t)u(t)\,dt. \end{aligned}$$

(A.1)

Its integral kernel K satisfies the equalities

$$\begin{aligned} K(x,x)=\frac{h}{2}+\frac{1}{2}\int _{0}^{x}Q(s)\,ds,\qquad K(x,-x)=\frac{h}{2}, \end{aligned}$$

(A.2)

and the derivative $\partial _{x}K=:K_{1}$ satisfies the equalities (see [18])

$$\begin{aligned}&K_{1}(x,x)=\frac{Q(x)}{4}+\frac{h}{4}\int _{0}^{x}Q(s)\,ds+\frac{1}{8}\biggl (\int _{0}^{x}Q(s)\,ds\biggr )^{2},\quad \nonumber \\&K_{1}(x,-x)=\frac{1}{4}\biggl (Q(0)+h\int _{0}^{x}Q(s)\,ds\biggr ). \end{aligned}$$

(A.3)

The integral kernel K is one degree smoother than the potential Q. To be more precise, let $Q\in W_{\infty }^{p}[0,b]$, $p\ge 0$, i.e., the function Q possesses p derivatives, the last one belonging to $L_{\infty }(0,b)$. In such case the integral kernel K possesses $p+1$ derivative with respect to each variable. In particular, for each $x>0$, $K(x,\cdot )\in W_{\infty } ^{p+1}[-x,x]$ and the norms $\Vert \partial ^{p+1}_{t} K(x,t)\Vert _{L_{\infty } (-x,x)}$ are bounded on [0, b].

The following result shows that the coefficients $\beta _{n}$ and $\gamma _{n}$ defined by (3.4) and (3.11) are the Fourier–Legendre coefficients of the integral kernel K and its derivative $K_{1}:=\partial _{x} K$, respectively.

Theorem A.1

[13] Let $Q\in L_{\infty }(0,b)$. The transmutation kernel K and its derivative $K_{1}$ have the form

$$\begin{aligned} K(x,t) = \sum _{j=0}^{\infty }\frac{\beta _{j}(x)}{x} P_{j}\left( \frac{t}{x}\right) \qquad \text {and}\qquad K_{1}(x,t) = \sum _{j=0}^{\infty }\frac{\gamma _{j}(x)}{x} P_{j}\left( \frac{t}{x}\right) , \end{aligned}$$

(A.4)

here $P_{n}$ denotes the classical Legendre polynomials. The coefficients $\beta _{n}$ and $\gamma _{n}$, $n\ge 0$, can be recovered using the formulas

$$\begin{aligned} \beta _{n}(x)= & {} \frac{2n+1}{2}\int _{-x}^{x} K(x,t) P_{n}\left( \frac{t}{x}\right) \,dt\qquad \text {and} \nonumber \\ \gamma _{n}(x)= & {} \frac{2n+1}{2}\int _{-x}^{x} K_{1}(x,t) P_{n}\left( \frac{t}{x}\right) \,dt. \end{aligned}$$

(A.5)

Denote by $K_{N}$ and $K_{1,N}$ partial sums of the series (A.4). Let $Q\in W_{\infty }^{p}[0,b]$, $p\ge 0$. Define

$$\begin{aligned} M:=\sup _{0<x\le b}\Vert \partial _{t}^{p+1} K(x,\cdot )\Vert _{L_{\infty }(-x,x)}\qquad \text {and}\qquad M_{1}:=\sup _{0<x\le b}\Vert \partial _{t}^{p} K_{1}(x,\cdot )\Vert _{L_{\infty }(-x,x)}. \end{aligned}$$

(A.6)

As was mentioned earlier, both suprema exist and are finite numbers. The following convergence rate estimates hold.

Proposition A.2

Let $Q\in W_{\infty }^{p}[0,b]$, $p\ge 0$. Then there exist constants $c_{p}$ and $d_{p}$ independent of Q and N, such that for all $x>0$ the following inequalities hold

$$\begin{aligned} \Vert K(x,\cdot )-K_{N}(x,\cdot )\Vert _{L_{2}(-x,x)}\le \frac{c_{p}Mx^{p+3/2} }{N^{p+1}},\qquad N\ge p+2, \end{aligned}$$

(A.7)

and

$$\begin{aligned} \Vert K_{1}(x,\cdot )-K_{1,N}(x,\cdot )\Vert _{L_{2}(-x,x)}\le \frac{d_{p} M_{1}x^{p+1/2}}{N^{p}},\qquad N\ge p+1. \end{aligned}$$

(A.8)

Proof

Let $x>0$ be fixed. Consider functions $g(z):=K(x,xz)$ and $g_{N} (z):=K_{N}(x,xz)$ defined on $[-1,1]$. The function $g_{N}$ is a partial sum of the Fourier–Legendre series for the function g, hence $g_{N}$ coincides with the N-th order polynomial best $L_{2}$ approximation of the function g. Since the integral kernel K possesses $p+1$ derivatives with respect to the second variable with the last derivative belonging to $L_{\infty }(-x,x)$, we have that $g\in W_{\infty }^{p+1}[-1,1]\subset W_{2}^{p+1}[-1,1]$. Theorem 6.2 from [5] states that there exists a universal constant $\tilde{c}_{p}$ such that for every $N>p+1$

$$\begin{aligned} \Vert g-g_{N}\Vert _{L_{2}(-1,1)}\le \frac{\tilde{c}_{p}}{N^{p+1}}\omega \left( g^{(p+1)},\frac{1}{N}\right) _{2}\le \frac{2\tilde{c}_{p}}{N^{p+1}}\Vert g^{(p+1)}\Vert _{L_{2}(-1,1)}, \end{aligned}$$

where $\omega$ is the modulus of continuity.

By the definition $g^{(p+1)}(z) = x^{p+1} \partial _{t}^{p+1}K(x,t)\big |_{t=xz} =:x^{p+1} K_{2}^{(p+1)}(x,xz)$, hence

$$\begin{aligned} \begin{aligned} \Vert K(x,\cdot )-K_{N}(x,\cdot )\Vert _{L_{2}(-x,x)}&= \sqrt{x}\Vert g-g_{N} \Vert _{L_{2}(-1,1)}\le \frac{2 \tilde{c}_{p} \sqrt{x}}{N^{p+1}} \Vert g^{(p+1)} \Vert _{L_{2}(-1,1)}\\&=\frac{2 \tilde{c}_{p} x^{p+3/2}}{N^{p+1}} \Vert K_{2}^{(p+1)}(x,x\cdot )\Vert _{L_{2}(-1,1)}\\&\le \frac{2\sqrt{2} \tilde{c}_{p} M x^{p+3/2}}{N^{p+1}}, \end{aligned} \end{aligned}$$

where we used that $\Vert K_{2}^{(p+1)}(x,x\cdot )\Vert _{L_{2}(-1,1)}\le \sqrt{2}M$ due to (A.6).

The second estimate (A.8) can be obtained similarly. $\square$

Estimates (A.7) and (A.8) provide upper bounds for the error functions $\varepsilon _{N}$ and $\varepsilon _{1,N}$ from Theorems 3.1 and 3.2. Indeed, the approximate solutions $c_{N}$ and $s_{N}$ are obtained by changing K by $K_{N}$ in (A.1). Hence by the Cauchy-Schwarz inequality we have

$$\begin{aligned} \begin{aligned} |c(\omega ,x)-c_{N}(\omega ,x)|&=\biggl |\int _{-x}^{x}\bigl (K(x,t)-K_{N} (x,t)\bigr )\cos \omega t\,dt\biggr |\\&\le \Vert K(x,\cdot )-K_{N}(x,\cdot )\Vert _{L_{2}(-x,x)}\cdot \biggl (\int _{-x}^{x}|\cos \omega t|^{2}\,dt\biggr )^{1/2}\\&\le \frac{\sqrt{2}c_{p}Mx^{p+2} }{N^{p+1}} \end{aligned} \end{aligned}$$

(A.9)

for any $\omega \in \mathbb {R}$. The estimates for the function $\varepsilon _{1,N}$ follows similarly by using corresponding estimates for the derivative $K_{1}$.

The following proposition provides estimates of the decay rate of the coefficients $\beta _{k}$ and $\gamma _{k}$ and their behavior near $x=0$.

Proposition A.3

Let $Q\in W_{\infty }^{p}[0,b]$, $p\ge 0$. There exist constants $C_{p}$ and $D_{p}$ (independent of N) such that

$$\begin{aligned} |\beta _{N}(x)|\le \frac{C_{p}x^{p+2}}{(N-1)^{p+1/2}},\qquad N\ge p+1 \end{aligned}$$

(A.10)

and

$$\begin{aligned} |\gamma _{N}(x)|\le \frac{D_{p}x^{p+1}}{(N-1)^{p-1/2}},\qquad N\ge p. \end{aligned}$$

(A.11)

Proof

We obtain using (A.5) and (A.7), the fact that the Legendre polynomial $P_{n}$ is orthogonal to any polynomial of degree less than N and the Cauchy-Schwarz inequality that

$$\begin{aligned} \begin{aligned} |\beta _{N}(x)|&=\frac{2N+1}{2}\biggl |\int _{-x}^{x}K(x,t)P_{N}\left( \frac{t}{x}\right) \,dt\biggr |\\&\le \frac{2N+1}{2}\int _{-x}^{x}\left| (K(x,t)-K_{N-1}(x,t))P_{N}\left( \frac{t}{x}\right) \right| \,dt\\&\le \frac{2N+1}{2}\Vert K(x,\cdot )-K_{N-1}(x,\cdot )\Vert _{L_{2}(-x,x)} \cdot \sqrt{\frac{2x}{2N+1}}\\&\le \sqrt{\frac{2N+1}{2}}\frac{c_{p}Mx^{p+2} }{(N-1)^{p+1}}. \end{aligned} \end{aligned}$$

The proof of the second estimate (A.11) is similar. $\square$

The following bound for the behavior of the first coefficients near $x=0$ is valid.

Corollary A.4

Let $Q \in W_{\infty }^{p}[0,b]$, $p\ge 0$. Then

$$\begin{aligned} |\beta _{n}(x)|&\le c_{n} x^{n+1}, \qquad n\le p+1, \end{aligned}$$

(A.12)

$$\begin{aligned} |\gamma _{n}(x)|&\le d_{n} x^{n+1},\qquad n\le p, \end{aligned}$$

(A.13)

where $c_{n}$ and $d_{n}$ are some constants dependent on Q.

Sufficient conditions for the smoothness of the transformed potential Q in terms of the coefficients p, q and r can be easily obtained from (2.4).