Effects of the Angle Between the Density Gradient and the External Magnetic Field on the Linear Mode Conversion and Resultant Beaming Angle of LO-Mode Radio Emissions

Abstract

Recent spacecraft’s observations of kilometric continuum radiation showed that the linear mode conversion theory (LMCT) cannot explain the beaming angle of these observations; on the other hand satellite observations show some local fluctuation in the density gradient. In this research, we consider the mode conversion process from UHR-mode (slow Z- mode) to LO-mode (ordinary) waves, focusing on the effect of the angle between the density gradient and the external magnetic field on the efficiency of the LMCT and the resultant beaming angle of converted LO-mode waves; a comparison of the LMCT and simulation results are presented. We first consider a condition that the density gradient is perpendicular to the external magnetic field, corresponding to the condition assumed in the conventional LMCT. Next, we extend the discussion to the condition that the density gradient is oblique to the external magnetic field. Our aim here is to investigate a condition where the efficient mode conversion can occur and to study the deviation of the beaming angle from that estimated by LMCT. From the results of analyses, for both perpendicular and oblique cases, the highest conversion efficiency is obtained for a certain value of the wave normal angle (critical wave normal angle) of the incident slow Z-mode waves, corresponding to the case when two mode branches are matched. The simulation results show in the perpendicular case that the beaming angle is consistent with the conventional LMCT; but in the oblique case a critical wave normal angle becomes different from the perpendicular case and the beaming angle is different from the LMCT prediction.

1 Introduction

The mode conversion of one type wave mode into another type of wave mode occurs in an inhomogeneous plasma and the associated irreversible transfer of wave energy to the mode conversion region is important (Stix 1992). The mode conversion, identified as a change of propagation modes of plasma waves, is one of the generation mechanisms of radio emissions occurring in an inhomogeneous plasma. The mode conversion of electrostatic waves to LO-mode (ordinary) waves has been investigated for the purpose of understanding the origin of planetary radio emissions.

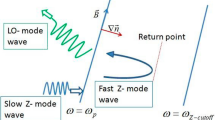
The considered mechanism for planetary radio emissions involves three processes (Oya 1971, 1974). In the first process, field–aligned precipitating beams and/or anisotropies of the velocity distribution of energetic electrons create electrostatic electron cyclotron harmonic waves (Warren and Hagg 1968). In the second process, the electrostatic electron cyclotron harmonic waves are converted to upper hybrid (UH) mode waves, propagating toward the region of higher plasma density. These waves are further transformed to the Z-mode radio waves toward the high density region. In the third process, a fraction of the Z-mode waves are reflected and then propagate into the plasma frequency layer of ω _p  = ω, (ω _p and ω represent the electron plasma frequency and the wave frequency, respectively), where these waves have a chance to convert into ordinary (LO-mode) waves.

There are some different types of mechanisms to explain the radiation of LO-mode waves from planetary magnetospheres, such as synchrotron radiation, linear mode conversion (Jones 1980), and nonlinear mode conversion. A typical example of escaping electromagnetic emissions is the nonthermal continuum radiation, which is one of the common radio emissions in planetary magnetospheres. The fundamental characteristics of observed continuum radiation have been explained by the mechanism proposed by previous studies (e.g., Jones 1980; Jones et al. 1987). (Jones et al. 1987; Jones 1988) applied the LMCW (linear mode conversion “window”) theory to explain the generation process of nonthermal continuum radiation. The prediction of LMCW is that the LO-mode radiation emanating from the radio window is beamed away from the magnetic equatorial plane at an angle given as follows (Jones 1988);

$$\beta_{LMCT} = \tan^{ - 1} \left( {\frac{{\omega_{c} }}{{\omega_{p} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,$$

(1)

where ω _c and β _LMCT represent the electron cyclotron frequency and the beaming angle from linear mode conversion theory (LMCT) prediction, respectively. The frequency of waves emitted from the radio window is determined by the local plasma frequency at the site of mode conversion. In general, we define β as the beaming angle with respect to the magnetic equatorial plane. MjΦlhus (1983, 1990) discussed the linear mode conversion of an ordinary polarized electromagnetic wave in a magnetized plasma with the density gradient parallel to the magnetic field. Kalaee et al. (2009, 2010) investigated the linear mode conversion process based on a simulation study. There is a vast literature on a large number of mode conversion phenomena involving many different wave modes, which we will not attempt to review here.

Recent satellite observations have indicated the beaming angle theory (Jones 1976, 1980; Jones et al. 1987) is not always consistent with these observations (Hashimoto et al. 2006; Boardsen et al. 2008). Also, satellite observations show some local fluctuation in the density gradient in the equatorial plasmasphere that leads to a variation of the angle between the external magnetic field and density gradient, which has not been studied in detail for the radio window theory (Grimald et al. 2007). These irregularities exist not only at the plasmapause but also inside the plasmasphere and in the notches, which are characterized by deep, mostly radial density depletions in the outer plasmasphere that extend inward to L = 2 or less.

In the present paper, we study the effect of the angle between the density gradient and the external magnetic field on the linear mode conversion and the resultant beaming angle of LO-mode radio emissions. We first discuss on the linear mode conversion from slow Z-mode (so-called UHR-mode waves in the frequency range defined by ω _p  < ω < ω _UHR , where ω _UHR represents the upper hybrid resonance frequency) to LO-mode waves under a condition that the density gradient is perpendicular to the external magnetic field. Then we extend the discussion to the condition that the density gradient is not perpendicular to the external magnetic field. Our aim here is to see the condition that the mode conversion can occur with a maximum efficiency and also to see whether the validity of the beaming angle theory will be protected or not. We discuss the conversion process by a cold plasma theory and also conduct numerical experiments by a cold electron fluid code to confirm our theory quantitatively. By employing numerical experiments, we show that the highest conversion efficiency is obtained at a certain wave normal angle of the incident waves. We also show the range of the critical wave normal angle, which depends on the plasma frequency, the wave frequency, and the angle α between density gradient and the external magnetic field. Finally, we show for the non-perpendicular case α ≠ 90° the beaming angle becomes different from Jones’ formula, given by (1).

2 Simulation Model

In the present study, we investigate the mode conversion process based on a cold plasma theory and then conduct numerical experiments by a cold electron fluid code to confirm our theory quantitatively. In this section, we briefly describe the simulation model used in our numerical experiments. We study the wave coupling process among slow Z- mode, fast Z-mode and LO-mode waves by using a spatially two-dimensional electron fluid code that was also used by Kalaee et al. (2009). The basic equations are given as follows:

$$\frac{{\partial {\mathbf{V}}}}{\partial t} = - ({\mathbf{V}} \cdot \nabla ){\mathbf{V}} + \frac{q}{Nm}({\mathbf{E}} + {\mathbf{V}} \times {\mathbf{B}})$$

(2)

$$\frac{\partial N}{\partial t} = - \nabla \cdot (N{\mathbf{V}})$$

(3)

$$\frac{{\partial {\mathbf{B}}}}{\partial t} = - \nabla \times {\mathbf{E}}$$

(4)

$$\frac{{\partial {\mathbf{E}}}}{\partial t} = \frac{1}{{\varepsilon_{0} \mu_{0} }}\nabla \times {\mathbf{B}} - \frac{1}{{\varepsilon_{0} }}{\mathbf{J}}$$

(5)

where E, B, J , V and N represent the electric field, the magnetic field, the current density, the velocity and the number density of the electron fluid, respectively. We solve the equation of motion (1) and continuity Eq. (3) coupled with Maxwell’s Eqs. (4–5) by using the two-step Lax-Wendroff scheme. Each physical value is normalized to a dimensionless quantity; time is normalized by the electron cyclotron frequency (ω _c ), velocity and length are normalized by the speed of light (c) and c/ω _c , respectively. We use the grid spacing ∆X and ∆Y of 1 × 10⁻² c/ω _c and a time step ∆t of 7.5 × 10⁻³ ωc ⁻¹. Figure 1 schematically indicates the two-dimensional simulation box used in the present study. The external magnetic field B ₀ is assumed to be in the X–Y plane with an angle θ against X-axis, and the angle between the density gradient and the external magnetic field is indicated by α. The simulation box consists of three regions: homogeneous regions with plasma frequencies of ω _PA (Region-A) and ω _PB (Region-B) smoothly connected by an inhomogeneous region. We generate plasma waves by oscillating Ex and Ez components in the wave generation region, while the wave vector k of generated waves is introduced to be aligned along the x- axis, that describes direction making an oblique propagating to the external magnetic field. To avoid any effects due to reflected waves from the boundary of the simulation box, we set damping regions at the edges of the simulation system so as to suppress the reflection of outgoing waves.

Fig. 1

Schematic of illustration of the simulation system. We assume homogenous regions with plasma frequencies of ω _PA (Region-A) and ω _PB (Region-B) smoothly connected by an inhomogeneous region where the density gradient ∇N is assumed with the spatial scale of ∆r. The width ∆r of the inhomogeneous region parallel to density gradient is about 8λ _Inc., where λ _Inc. is the wavelength of incident waves

3 Results and Discussion

3.1 Case1: Perpendicular Case

We first consider a case that the external magnetic field is assumed perpendicular to the density gradient. We consider a typical example of the mode conversion process from slow Z-mode waves to LO-mode waves. We assume ω _PA /ω _c  = 2.0 and ω _PB /ω _c  = 2.54. We also assume that the incident wave frequency is ω = 2.03 ω _c , which is close to plasma frequency in the Region-A and is smaller than the Z-mode cutoff frequency in the Region-B.

In the simulation results, we observed the generation of LO-mode waves through the mode conversion process. In order to examine the coupling properties between slow Z-mode and LO-mode waves, we performed Fast Fourier Transform (FFT) analyses on the tree components of both wave electric field and magnetic field. Based on the obtained wavenumber and frequency spectra, we estimated the wave normal angle of the converted LO-mode waves by comparing the ratio of the wave electric field components E _x /E _Z and E _y /E _Z in the simulation results with those estimated from the dispersion relation of LO-mode waves. Before discussion of the parameter dependence, we show a typical example of the mode conversion process reproduced in simulation results shown in Fig. 2. Here we assumed θ = 58.3°, where θ is the wave normal angle of the incident wave. In the case of the transmission from slow Z-mode (UHR-mode) to fast Z-mode waves (ω _Z-cutoff  < ω < ω _p , where ω _Z-cutoff is the Z-mode cut-off frequency), a part of the incident slow Z-mode waves are transmitted into fast Z-mode waves over the location where ω = ω _p in the inhomogeneous medium, while other part of wave energy are reflected toward the Region-A as slow Z-mode waves. Under the present condition, however, the transmitted waves cannot propagate further into the Region-B, because the wave frequency is lower than the cutoff frequency of Z-mode waves in the Region-B. Therefore the transmitted fast Z-mode waves are eventually reflected when they encounter the local cutoff frequency and meet again the condition where the wave frequency becomes ω = ω _p , resulting in the mode conversion from Z-mode to LO-mode waves (Kalaee et al. 2009). Figure 2a, b respectively indicate the spatial distributions of the Ex component at t = 52.5 ω ⁻¹ _c and t = 157 ω ⁻¹ _c , respectively correspond to the time intervals before and after the mode conversion process which occurred around t = 60 ω ⁻¹ _c . We can clearly observe the LO-mode waves in Fig. 2b. By analyzing the polarization of the LO-mode waves, we obtained Ex/Ez ≈ 1.73, kx ≈ 0.4, and ky ≈ 1.03, where kx and ky represent the x and y-components of the wave vector, respectively, and we estimated that the wave normal angle of the converted LO-mode wave is nearly 8° respect to the ambient magnetic field.

Fig. 2

Spatial distribution of the Ex component of the electric field in the simulation system for the perpendicular case, showing the entrance of incident waves to the inhomogeneous region at (a) t = 52.5 ω ⁻¹_c and the propagation of the converted LO-mode waves away from the inhomogeneous region at (b) t = 157 ω ⁻¹_c

3.1.1 Dependence on Wave Normal Angle

Kalaee et al. (2009) studied the dependence of the mode conversion efficiency on the wave normal angle and the background plasma frequency for the perpendicular case. For a better understanding of the mode conversion conditions, here we represent some results in this case and then in Sect. 3.2 we will extend the discussion to the condition that the density gradient is not perpendicular to the external magnetic field. By assuming the same background plasma condition as used in the result of Fig. 2, we perform five simulation runs (Run A to E) with different propagation angles. The assumed propagation angle and simulation results are summarized in Table 1, while the initial settings used in Fig. 2 correspond to Run C of Table 1. Table 1 consists of the wave normal angles of the incident waves and the converted LO mode waves in Region-A in the simulation box, the frequency of the incident waves, the ratio of the electric field components obtained from the simulation results and those estimated from the dispersion relation, and the mode conversion efficiency. We define the mode conversion efficiency by the ratio of the Poynting vector of LO mode wave to the Poynting vector of the incident wave. By analyzing the simulation results, we examine the coupling properties between slow Z-mode (UHR-mode) and LO-mode waves. The obtained conversion efficiency as a function of the incident wave normal angle is shown in Fig. 3. As shown in Fig. 3, the highest conversion efficiency was obtained in Run C and the conversion efficiency decreased exponentially with varying the incident propagation angle. Figure 3 also shows that the efficiency becomes highest at the certain incident wave normal angle. In this study, we focus on the highest conversion efficiency case.

Table 1 Summary of simulation results and parameters used in Case 1, consist of wave normal angles of incident waves and converted LO-mode waves, the frequency of the incident waves, the ratio of electric field components, and the mode conversion efficiency based on the ratio of the Poynting vectors of two modes

Fig. 3

Variations of the conversion efficiency depending on the wave normal angle of the incident slow Z-mode waves for the perpendicular cases. Each point corresponds to the results obtained by runs A to E. The maximum value corresponds to the matching case

3.1.2 Summary and Discussion on Case 1

In the simulation results of the Case 1, we considered a perpendicular case and we found that the conversion efficiency of the mode conversion process strongly depends on the wave normal angle of the incident waves. This tendency is commonly found in the simulations assuming the different plasma frequency in the simulation system. This means, even if the plasma frequency changes, the highest mode conversion efficiency can be realized at a certain incident wave normal angle. The value of the highest mode conversion efficiency is almost the same with the results obtained in Run C. Here we discuss the coupling properties of Z and LO-mode waves in detail based on the cold plasma theory. By considering the dispersion relation for waves in a cold plasma, we obtain.

$$n^{2} = n_{||}^{2} + n_{ \bot }^{2} = 1 - \frac{2X(X - 1)}{{2(X - 1) - Y^{2} \sin^{2} \theta \pm \varGamma }}$$

(6)

where n is the refractive index, yn _|| and yn _⊥ are the parallel and perpendicular components of the refractive index, respectively,

$$\varGamma = [Y^{4} \sin^{4} \theta + 4(X - 1)^{2} Y^{2} \cos^{2} \theta ]^{1/2}$$

(7)

$X = \left( {\frac{{\omega_{p} }}{\omega }} \right)^{2}$, $Y = \frac{{\omega_{c} }}{\omega }$, θ is the angle between the wave vector (k) and the external magnetic field (B₀), and the + (−) sign gives the refractive index of the Z- (LO-) mode. By considering Snell’s law and the assumption that the external magnetic field is directed perpendicular to the density gradient, the parallel component of the refractive index should be constant during the wave propagation in an inhomogeneous medium.

It is also clear from Eq. (6) that the two modes coalesce when the quantity Γ vanishes. This in turn requires that the conditions of X = 1 and θ = 0 should be simultaneously satisfied. The condition of θ = 0, namely that n _⊥, _LO  = n _⊥, _Z  = 0_, where n _⊥, _LO and n _⊥, _Z are perpendicular components of the refractive index of LO-mode and Z-mode waves respectively. Base on this discussion, we can estimate the parallel component of the refractive index of the incident slow Z-mode wave corresponding to the highest conversion efficiency in the mode conversion process by referring the value of.

$$\left( {n_{||}^{c} } \right)^{2} = \frac{Y}{1 + Y}$$

(8)

where yn ^c_|| is a critical value for the parallel component of the refractive index.

We found that the estimations based on the theory are consistent with the simulation results. The parallel components of the refractive index of both LO mode and slow Z-mode waves have the same value, equals to (Y/1 + Y)^1/2 for the wave parameters corresponding to the highest conversion efficiency. In this case, at the point of the mode conversion, the perpendicular components of the refractive index of waves are matched. For example, in Fig. 3, we obtained the highest conversion efficiency when ω = 2.03 ω _c and θ = 58.3°. Meanwhile, the estimated critical value for the wave frequency of ω = 2.03 ω _c is (n ^c_|| )² = (0.5745)², corresponds to θ = 58.3° which is consistent with the simulation setting. Figure 4a shows θ determined from the dispersion relation as a function of ω _p /ω _c for LO (ordinary) mode and Z- (extraordinary) mode waves for the case of n _|| = n ^c_|| .

Fig. 4

Variation of the wave normal angle θ for the perpendicular case. The black circles show the incident wave normal angles at which the waves are injected. a Three examples of the matching cases. Under these settings, the conditions in which both n _|| = n ^c_|| and $n_{{ \bot ,{\text{LO}}}} = n_{{ \bot ,{\text{Z}}}} = 0$ are satisfied at θ = 0 as shown by the points A, B and C in the diagram. By matching two modes, the efficient mode conversion can occur. b Three examples of the mismatching cases corresponding to the condition that n _|| ≠ n ^c_|| is satisfied at the location of the mode conversion for incident waves of ω = 2.03 ω_c with different wave normal angles of θ = 64° (red curve), θ = 50° (blue curve), and θ = 42° (green curve). In each case, arrow shows an evanescent region between Z- mode and LO mode waves. (Color figure online)

Figure 4a shows three examples of the matching cases, when the wave frequency matches the local plasma frequency. In each case two curves (Z mode and LO mode waves) match at the region where ω _p /ω _c is equal to ω/ω _c . The coupling between these two modes can strongly occur at the points A, B and C. That is, two branches match each other for incident waves of a wave normal angle θ = 50° and the wave frequency of 1.05 ω _c in the region of ω _p /ω _c  = 1 (corresponding to the point A), for θ = 58.3° and ω/ω _c  = 2.03 in the region of ω _p /ω _c  = 2.0 (the point B), and for θ = 64° and ω/ω _c  = 3.03 in the region of ω _p /ω _c  = 3.0 (the point C). Note that, in a case that n _|| ≠ n ^c_|| , the curves of the LO and Z mode branches are mismatched for a real value of n _⊥. This mismatch results in the decrease of the mode conversion efficiency. Two typical examples are shown in Fig. 4b. If n _|| ≠ n ^c_|| , the LO- mode and Z-mode branches do not meet for real values of n. A region of evanescence develops between the two branches, and the mode conversion can only takes place by the effect of tunneling through the evanescent region. The tunneling efficiency was investigated by generalizing the work of Perinhaelter and Kopecky (1973).

3.2 Case2: Non-Perpendicular Case

Next, we discuss a condition that the density gradient is not perpendicular to the external magnetic field direction. Under this condition, the ordinary and extraordinary mode branches meet for real values of n _⊥. For a case that the density gradient is set perpendicular to magnetic field direction, two branches of LO-mode and Z-mode waves meet together when n cos θ = n _|| = n ^c_{|| ,} while k cos θ should be constant. In the case that the angle between the density gradient and the external magnetic field direction is α ≠ π/2, k cos (π/2 − α + θ) should be constant. Figure 5 shows the schematic diagram of the k vector with respect to the external magnetic field and the boundary surface in a plasma medium where (a) the density gradient is set perpendicular to the external magnetic field direction and (b) the density gradient is set oblique to the magnetic field direction. In the cases (a) and (b) k cos θ and k cos (π/2 − α + θ) should respectively be constant according to Snell’s law.We extend the case that α = 90° to a case that α ≠ 90° by.

$$n\;\sin (\alpha - \theta ) = \left( {\frac{Y}{1 + Y}} \right)^{1/2} \sin \;\alpha ,$$

(9)

where two branches of LO-mode and Z-mode waves can be matched (see Fig. 8). When α = 90°, (9) becomes n cos θ = n _|| = n ^c_|| .

Fig. 5

Schematic diagram of the wave vector k in a plasma medium. According to Snell’s law, the tangential component of k should be constant. a The density gradient is set perpendicular to the magnetic field direction and b the density gradient is set obliquely with respect to the magnetic field direction. The angle between the wave vector k and the external magnetic field direction is θ (θ ≤ α)

In order to examine the case of α ≠ 90° and to compare with the perpendicular case, we perform a simulation by assuming ω = 2.03 ω _c , ω _pA  = 2.0 ω _c , α = 70°, and θ = 42.3° so as to satisfy the above condition (Eq. (9)). Figure 6 shows the spatial distribution of the wave electric field amplitude obtained from the simulation result. The simulation results indicate the mode conversion occurred and the efficiency of mode conversion is estimated to 0.55. We perform three simulation runs (Run F to H) with different propagation angles. The assumed propagation angle and simulation results are summarized in Table 2, while the initial settings used in Fig. 6 correspond to Run F of Table 2. Runs F and G correspond to the matching case and Run H corresponds to the mismatching case. These results show that, two branches of LO-mode and Z-mode waves can couple only in a case that Eq. (9) is satisfied and so the efficiency becomes the maximum value. We obtain almost the same conversion efficiency of 0.55 in the simulation results of Runs C, F, and G, respectively satisfying the condition of Eq. (9) (matching cases) for different α. Based on this exploration and the results of the simulation, we can estimate the incident angle corresponding to the highest efficiency. Figure 7 indicates the relation among the wave frequency, the incident wave normal angle and the background plasma frequency (at the initial homogeneous region), which leads to the most efficient mode conversion for α equals 90 (dash lines) and 70 (solid lines) degrees, respectively. Figure 7 indicates that the incident wave normal angle satisfying the condition of Eq, (9) decreases with decrease of α.

Fig. 6

Spatial distribution of the Ex component of the electric field in the simulation system for the non-perpendicular case, with ω = 20.03 ω _c, α = 70° and θ = 42°. The mode conversion efficiency becomes the maximum value in the assumed condition

Table 2 Summary of simulation results and parameters used in Case 2, consist of wave normal angle, incident frequency, ratio of electric field components and mode conversion efficiency

Fig. 7

Variations of the wave normal angle θ satisfying the condition of n _|| = n ^c_|| as a function of the local plasma frequency at the initial homogeneous region for α = 90° (dash lines) and α = 70° (solid lines). Each curve shows the contour line of the wave frequency normalized by the gyrofrequency. The contour lines are drawn every 0.01 ω _p

3.3 Discussion on the Beaming Angle and Efficiency

The beaming angle as a prediction of LMCT is important, but this prediction is not always consistent with observation. We consider the beaming angle of radio waves based on the results of the present study. Using the estimated wave normal angle and assuming Snell’s law during the propagation of LO-mode waves toward the region of the lower plasma frequency, we estimate the beaming angle of the LO-mode waves at the region away from the site of the mode conversion. Figure 8 shows the variations of the wave normal angle with the constant k cos (π/2 − α + θ)as a function of ω _p /ω _c under the condition of Case 1 (α = 90) and Case 2 (α = 70). In each result, the wave normal angle increases during the propagation toward the lower density region and approaches to a certain value corresponding to the propagation angle of LO-mode waves in the free space. We can obtain the beaming angle β with respect to the magnetic equatorial plane by β = (90 – θ), where θ is the wave normal angle of LO-mode waves. As shown in Fig. 8, we find that θ approaches a certain value as the plasma density decreases and eventually obtain the asymptotic value of θ, corresponding to the propagation angle of LO-mode waves in free space. We obtain θ ≈ 55° of LO-mode waves in Case 1(green curve), corresponding to the beaming angle β1 ≈ 35°. On the other hand, for a plasma frequency ω _p  = 2.03 ω _c at the mode conversion point, we obtain $\beta_{LMCT} = \tan^{ - 1} \left( {\frac{{\omega_{c} }}{{\omega_{p} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \approx 35.1^{^\circ }$. For this case, the estimated beaming angle (β1) is consistent with that predicted by the Jones’ formula (1). Next, we examine the result of Case 2 (blue curve). As shown in Fig. 8, we obtain the convergent wave normal angle θ ≈ 37° of LO-mode waves, corresponding to the beaming angle β2 ≈ 53°. For this case, the beaming angle (β2) becomes larger than that estimated from Jones’ formula, which is the same value as we obtained for Case 1 because of the same ω _p /ω _c at the site of the mode conversion. Figure 9 indicates the relation among the beaming angle of LO-mode wave and background plasma frequency at the conversion point under the condition corresponding to the most efficient mode conversion for α equals 90°, 80°, and 70°, respectively. In non-perpendicular cases, there is a certain wave normal angle of incident waves that two branches of Z- and LO-mode waves can match each other and that the mode conversion efficiency becomes maximum, but it results in the beaming angle different from estimations of the Jones’ formula.

Fig. 8

Variations of the wave normal angle θ as a function of the local plasma frequency. Both curves (green and blue) show the matching cases. Green and blue curves respectively correspond to α = 90° and α = 70°. Two circles on the curves indicate the settings used in the simulation runs. We can estimate the beaming angle beta by β = 90–θ by using the asymptotic value of theta in the small ω _p /ω _c range. We thereby obtain the beaming angle for each case as β₁ = 35° and β₂ = 53°. (Color figure online)

Fig. 9

The relation among the beaming angle β of LO-mode wave and ω _p /ω _p at the conversion point, which leads the most efficient mode conversion for α equals 90°, 80°, and 70°, respectively. The curves show the beaming angle increases with the decrease of α

In the perpendicular case (α = 90°),the efficiency becomes the maximum value (about 0.55) for the matching case, while for mismatching cases the efficiency rapidly decreases to zero. These results reveal that the mode conversion occurs only for waves incident within a very narrow angle around the critical angle. In the non perpendicular cases (α ≠ 90°),the efficiency also becomes the maximum value (about 0.55) for the matching case but with different incident wave normal angles depending on α. For the mismatching cases, again the efficiency rapidly decreases to zero as we found in the perpendicular case. A summary of discussion is listed below:

• 1. Under the matching case, for both the perpendicular and the non perpendicular cases, the efficiency becomes the maximum value.

• 2. In the mismatching case, for both the perpendicular and the non perpendicular cases, the efficiency rapidly decreases to zero as the wave normal angle of incident waves deviates from the critical angle that leads to the maximum efficiency.

• 3. For different α, the critical angle varies accordingly.

• 4. In the matching case, the beaming angle increases with decrease of α.

4 Summary

In the present paper, we studied the properties of the mode conversion processes using two dimensional electron fluid simulations.

Firstly, we considered the case that the external magnetic field is assumed perpendicular to the density gradient and we obtained high conversion efficiencies in this coupling process. We also performed the theoretical estimation of the conversion process by analyzing the dispersion relation of the cold plasma. We confirmed that the maximum conversion efficiency obtained in the simulation results is explained by the matching of the perpendicular component of the refractive index of waves at the site of the mode conversion, when the parallel component of the refractive index of the incident waves is equal to $\left( {\frac{Y}{1 + Y}} \right)^{1/2}$. We showed in the perpendicular case and the settings satisfying the matching condition that the beaming angle is consistent with the prediction by Jones’ formula. In a case that the parallel component of the refractive index of incident waves is slightly different from the critical value of the refractive index $\left( {n_{||} \neq \left( {\frac{Y}{1 + Y}} \right)^{1/2} } \right)$, two branches are mismatched and there is an evanescent layer even though the perpendicular component of the refractive index becomes zero for both LO-mode and Z-mode waves. Although the LMCT predicts that the mode conversion does not occur in such a case, the recent simulation results by Kalaee et al. (2009) have shown that the effective mode conversion can be expected where the spatial scale of the density gradient is the order of one wavelength_.

Secondly, in Case 2, we considered a condition that the density gradient is not perpendicular to the external magnetic field direction. By employing numerical experiments and by calculating the ratio of Poynting vector of each wave mode, we showed that the highest conversion efficiency is obtained when the incident wave normal angle satisfies Eq. (9). We also showed that the range of the critical normal angle varied depending on the plasma frequency, the wave frequency, and the angle between density gradient and the external magnetic field (α). Finally, we showed for the non-perpendicular case (α ≠ 90°) the beaming angle does not correspond to Jones’ formula. Figure 8 show the beaming angle increases with decreases in α.

These results suggest a possibility that the beaming angle of LO-mode waves propagating in the magnetosphere is different from that of the LMCT prediction. Numerical simulation showed that the mode conversion with a maximum rate takes place not only in a case that α = 90° but also in a case that α ≠ 90°. These results can be applied to the equatorial region of the plasmapause in the Earth’s inner magnetosphere during geomagnetically disturbed periods and the case of field-aligned irregularities in the polar region of the magnetosphere, where we can expect that the density gradient becomes steep and is not purely perpendicular to the external magnetic field direction. In order to apply these results, we need to detailed plasma environments from spacecraft observations such as the plasma frequency, the cyclotron frequency, the wave frequency of radiation, the beaming angle, and the angle between the density gradient and the external magnetic field. By assuming initial plasma settings inferred from observation data, we can discuss the process under a realistic condition. By knowing the wave frequency of LO mode waves and the angle between the density gradient and the magnetic field from observation, we can compare our results with the observed beaming angle; such studies will be important in the future study.