1 Introduction

Wrinkle ridges are simple linear to sinuous geological structures with positive reliefs and are mainly distributed in lunar mares; only a few can be found in nearby highlands (Strom 1972). Although lunar wrinkle ridges have been comprehensively studied to understand their formation processes, distribution characteristics or other properties, some disagreements still exist regarding their formation mechanisms. Previous studies suggested that the wrinkle ridges were mainly formed by volcanism intrusive and/or extrusive (e.g., Strom 1972; Hodges 1973), tectonic faulting and/or folding (e.g., Bryan 1973; Golombek et al. 1991; Watters and Schultz 2010), or combinations of tectonic and volcanic processes (e.g., Young et al. 1973; Scott et al. 1975; Maxwell et al. 1975). However, by analyzing a large number of similar structures on the terrestrial surface and from radar data, many researchers consider the origin of wrinkle ridges to be more likely due tectonic processes (e.g., Plescia and Golombek 1986; Watters 1988; Ono et al. 2009).

In addition, many researchers have mapped the wrinkle ridges and analyzed their distribution characteristics (e.g., Maxwell et al. 1975; Fagin et al. 1978; Golombek et al. 1991; Walsh et al. 2013; Yue et al. 2015; Thompson et al. 2017). Through analyzing the previous mappings of wrinkle ridges and their distribution characteristics on the lunar surface, we can find that wrinkle ridges are more likely distributed in or around the lava-filled mares than the highlands and have certain regional characteristics in their distributions: (1) parallel to each other with a regionally uniform orientation in the lunar mare and tending to be parallel to the trends of the lunar grid system (Strom 1964); (2) concentric or radial to the corresponding centre of a clear circular or elliptical mare or basin; (3) geographically scattered or isolated on the lunar surface. The regional distribution characteristics of wrinkle ridges can indicate the tectonic patterns of an area and the force trends that formed these structures, especially for the concentric or radial groups distributed in lunar mares. For these features, the regional characteristics can reflect their formation modes and the orientations of their stress field at the time of their formation.

However, most previous studies qualitatively identified whether the wrinkle ridges were distributed concentrically, radially or not instead of using a quantitative method in their analysis. For this reason, this paper aims to introduce a quantitative method to analyze the distribution characteristics of those wrinkle ridges which are concentrically or radially oriented in a circular lunar mare using a parameter called the central symmetry value (Johnson 1974; Liu 1985) to better understand the formation modes and stress fields of wrinkle ridges.

2 Data and Background Description

2.1 Data

A mosaic images and topographic data of Mare Serentatis (5°–35°E, 15°–42°N) acquired by the Lunar Imager/SpectroMeter (LISM) instrument onboard the SELENE (KAGUYA) spacecraft were used in this study. The LISM instrument consists of three payloads: the Terrain Camera (TC), the Multiband Imager (MI) and the Spectral Profiler (SP). The Terrain Camera (TC) is a push-broom imaging camera with a spatial resolution of 10 m/pixel from a SELENE altitude of 100 km (Ohtake et al. 2008; Haruyama et al. 2009), and stereo images of TC provide a global map of digital terrain models (DTMs) with the same resolution as the TC image.

In this paper, 110 evening images of the TC data are mosaicked to identify and map the wrinkle ridges; 110 DTM tiles are merged to assist in mapping wrinkle ridges and analyzing the topographical characteristics of the wrinkle ridges. All images are mosaicked by the ENVI platform after downloading from the SELENE Data Archive (http://l2db.selene.darts.isas.jaxa.jp/index.html.en).

2.2 Background

2.2.1 Geological Settings of Mare Serenitatis

Mare Serenitatis (26°N, 18°E) is one of the prominent lunar mares on the eastern near side of the Moon and was formed in the Nectarian era with a diameter of ca.740 km (Fig. 1a) (Head 1979; Wilhelms et al. 1987). The mare is close to circular in morphology, displays a mascon, and formed many types of features related to tectonic processes, such as rilles and wrinkle ridges. In addition, Mare Serenitatis apparently has two processes that influenced its evolution: impact cratering and mare volcanism (Head 1979). Mare Serenitatis not only possesses plenty of wrinkle ridges but also the wrinkle ridges occur in a concentric or radial pattern, which can satisfy the aims of this study. Thus, Mare Serenitatis was selected as a study area for this paper to analyze the distribution characteristics and central symmetry degrees of the wrinkle ridges in the lunar mare.

Fig. 1
figure 1

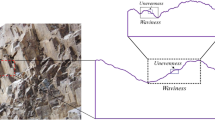
a Terrain Camera mosaic image of Mare Serenitatis with the five ridge systems proposed by Maxwell et al. (1975). The solid and dashed lines that the white arrows point to are no data areas. b Wrinkle ridge image of TC. c Topography of a wrinkle ridge from DTM. d Elevation profile of AA’ derived from DTM

Full size image

2.2.2 Morphology of Wrinkle Ridge

Wrinkle ridges, also called mare ridges, are complicated linear to sinuous tectonic features which are mainly located in mare basalt. Typical wrinkle ridges have two parts: a broad, gentle arch and a comparatively sharp, steep ridge (Strom 1972). The wrinkle ridges distributed in lunar mares were generally considered to originate from faulting and/or folding tectonic process in the basin (Maxwell et al. 1975). In remote sensing data (Fig. 1a, b), the morphology of wrinkle ridges appear as discontinuous rope, braids or irregular vein types, and their distribution patterns can be classified into isolated, clustered, parallel or circular distributions. In topographic data and terrain profiles (Fig. 1c, d), wrinkle ridges show positive relief terrain with a broad arch and a comparatively sharper ridge. The arch uplift is relatively gentle, and the ridge is steep.

2.2.3 Previous Studies of Wrinkle Ridges in Mare Serenitatis

Due to the wrinkle ridges being one of the most common features in Mare Serenitatis, many researchers have studied their distribution characteristics, formation processes and other properties (e.g., Maxwell et al. 1975; Fagin et al. 1978; Golombek et al. 1991; Yue et al. 2015; Thompson et al. 2017). Previous studies proved that the vast majority of wrinkle ridges are concentrically or radially distributed in Mare Serenitatis. Among these studies, Maxwell et al. (1975) summarized the observations of lunar wrinkle ridges and suggested that there exist five dominant trends of the ridge systems in this lunar mare: (1) a dominant orientation that is coincident with the inner ring of the Serenitatis basin, as determined by Wilhelms and McCauley (1971) (Fig. 1a–A, 400 km in diameter); (2) a circular ridge system in the east of the Bessel crater with a 140 diameter (Fig. 1a–B); (3) a northeastern system distributed at the northern boundary of Serenitatis (Fig. 1a–C, 330 km in diameter); (4) a ridge system present to the west of the northeast region (Fig. 1a–D, 250 km in diameter) and (5) a ridge system that mark the boundary of a topographic bench in the western Mare Serenitatis. According to the purpose of this paper, these five ridge systems of wrinkle ridges were used and analyzed in the following sections.

3 Methodology

3.1 Mapping and Distribution of Wrinkle Ridges

Based on previous studies and the morphological characteristics of wrinkle ridges as well as considering the purpose of this paper, we used two methods to map the wrinkle ridges distributed in Mare Serenitatis from TC mosaic image with combination of DTM images. The first method of mapping wrinkle ridges is tracing the centreline of the wrinkle ridge assemblage along their strike (Thompson et al. 2017); the second method to map wrinkle ridges is that using an approximately minimum bounding rectangle along its orientation to represent the wrinkle ridge segments based on the condition of each segment having similar strikes and widths (Yue et al. 2015).

In the current paper, we mapped 123 wrinkle ridges using the first method (Fig. 2a) and 501 segments using the second method (Fig. 2b). From the distribution map of the wrinkle ridges in Mare Serenitatis (Fig. 2), we can see that the wrinkle ridges are overall concentrically distributed and correspond to the centre of Mare Serenitatis with some obvious distributed trends. Between the highland and mare basalt, the wrinkle ridges are distributed along the boundary except those lying northeastward, which are parallel to the highland direction. Beside these wrinkle ridges, there are some wrinkle ridges distributed along in north–south direction.

Fig. 2
figure 2

Distribution map of wrinkle ridges in Mare Serenitatis. a Distribution map of wrinkle ridges extracted along the centreline of their strike. Inset: example of the first method. b Distribution map of the wrinkle ridges extracted by approximately the minimum bounding rectangle (indicated by white rectangles) along the segment orientation. Inset: example of second method

Full size image

3.2 Calculation of Central Symmetry Value

To study the regional characteristics of lineaments, Johnson (1974) introduced a mathematical filter to identify the potential presence of subsurface structural and stratigraphic anomalies. He used the standard deviation of the linear feature orientations in per unit areas to analyze the regional lineaments. The higher the degree of central symmetry of the linear features, the larger the standard deviation of the linear feature orientations, and the dominant orientation would be less obvious. Based on the study of Johnson (1974), Liu (1985) made a refinement of this method to statistically analyze the degree of central symmetry of those lineaments extracted from remote sensing images. This method was widely used to analyze the degree of central symmetry of terrestrial linear features but was barely used in lunar lineaments analysis. For this reason and according to the purpose of the lineament central symmetry statistical analysis method, we used this method in our study to detect the degree of central symmetry of the wrinkle ridges in Mare Serenitatis and to understand their mode of formation or the influence of the evolutions of the wrinkle ridges. The equations used to calculate the central symmetry value are

$$\sigma = \left[ {{{\sum\nolimits_{i = 1}^{n} {l_{i} \sin^{2} (\theta_{i} - \bar{\theta })} } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {l_{i} \sin^{2} (\theta_{i} - \bar{\theta })} } {\sum\nolimits_{i = 1}^{n} {l_{i} } }}} \right. \kern-0pt} {\sum\nolimits_{i = 1}^{n} {l_{i} } }}} \right]^{{\frac{1}{2}}}$$
(1)
$$\bar{\theta } = {{\sum\nolimits_{i = 1}^{n} {l_{i} \theta_{i} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {l_{i} \theta_{i} } } {\sum\nolimits_{i = 1}^{n} {l_{i} } }}} \right. \kern-0pt} {\sum\nolimits_{i = 1}^{n} {l_{i} } }}$$
(2)

where σ is the central symmetry value, \(0 \le \sigma \le {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. \kern-0pt} 2};\) \(\overline{\theta }\) is the average orientation of the wrinkle ridges and the unit is degree (°); l i is the wrinkle ridge’s length of i in each grid with a unit of km, i = 1, 2, 3,…n; θ i is the wrinkle ridge’s orientation of i in each grid with a unit of degree (°), − 90° ≤ θ i  ≤ 90°.

In the equations, there are two important parameters of each wrinkle ridge that need to be measured: length and orientation. However, the values of length and orientation will cause discrepancies when using different methods to measure them. To assess the bias of the central symmetry value caused by these two parameters, we used different approaches to measure and calculate the wrinkle ridges’ lengths and orientations. Noting that the orientation and length of wrinkle ridges used to calculate the central symmetry value are based on the grid size of the study area, the determination of the grid size is also an important factor in calculating the central symmetry value.

3.2.1 Length Measurement of Wrinkle Ridges

Due to the complicated morphologies of wrinkle ridges, there are many methods to measure the lengths of these features (e.g., Chabot et al. 2000; Hurwitz et al. 2013; Yue et al. 2015). To analyze the length discrepancies of wrinkle ridges caused by different methods, we took one wrinkle ridge as an example to explain and assess the discrepancy of the measured length that caused by using different methods (Fig. 3a). However, the length of each wrinkle ridge is correlated with map projection; so, to minimize the distortion of the wrinkle ridge’s length resulted by map projections, we used a spherical coordinates and independent projection to calculate the lengths of wrinkle ridges according to the locations of study areas (Kneissl et al. 2011).

Fig. 3
figure 3

Example of length calculation of a wrinkle ridge. All the images are in the equidistant cylindrical projection centred at 25°E, 28°N. a Wrinkle ridge from TC image. b Two walls of wrinkle ridge extracted by method L1. c Five segments mapped using method L2. The white rectangles indicate the divided segments of the wrinkle ridge, and the yellow lines are the lengths of each segment

Full size image

In this study, we used two methods to measure the lengths of the wrinkle ridge. The first method (named L1) to measure the length is defined as the average length of the wrinkle ridge’s two walls along its strike; each wall was mapped individually, the calculated lengths for the walls were averaged, and the uncertainty of the measured length is taken as the standard deviation of the two walls length (Fig. 3b) (Hurwitz et al. 2013). The second method (named L2) to measure the length of a wrinkle ridge was established by using an approximately minimum bounding rectangle along the features orientation. In this method, one wrinkle ridge is divided into segments with the condition that each segment has at least a similar strike and width; the length of the wrinkle ridge is the total length of the segments represented by the longer dimension of the corresponding rectangles (Fig. 3c) (Yue et al. 2015). Using these two methods, we automatically calculated the lengths of wrinkle ridges by ArcGIS after projection. The detailed information of the wrinkle ridge lengths measured by the two methods was listed in Tables 1 and 2, respectively.

Table 1 Length measurement of wrinkle ridge by method L1
Full size table
Table 2 Length measurement of wrinkle ridge by method L2
Full size table

The lengths of the wrinkle ridge measured by method L1 and method L2 are 25.62, 22.67 km, respectively, and the bias is 2.95 km. This example shows that the complicated morphology of wrinkle ridges and the different methods used to measure the lengths of wrinkle ridges can cause length deviations for the same wrinkle ridge. In this example, the length measured by method L1 is greater than that of method L2 due to the sinuous nature of the wrinkle ridge. However, the impact on the accuracy of the central symmetry value calculation caused by length deviation will be discussed in Sect. 4.

3.2.2 Orientation Measurement of Wrinkle Ridge

The orientation of a set of wrinkle ridges can indicate the predominant stress fields that formed these features, but the orientations calculated by different methods show deviations. For this reason, we used two methods to measure the orientation of each wrinkle ridge in our research. Like the length calculation, the map projection has a profound influence on the orientation calculation. Thus, for the orientation of the wrinkle ridge to keep conformal, the wrinkle ridges were mapped by Mercator projection independently.

For the first method (named O1), the orientation of the wrinkle ridge was defined as the average orientation of the wrinkle ridge’s two walls along its strike, and the orientation of each wall was determined by the coordinates of the endpoints of each wrinkle ridge after its map projection (Fig. 4a). The second method (named O2) was designed by Yue et al. (2015), and the orientation of the wrinkle ridge was calculated using all the segment orientations after weighting by the lengths of each segment. The orientation of each segment was calculated as the angle between the north trend and the central line of each rectangle segment (Fig. 4b). The orientation range of these two methods is between − 90° and 90°. 0° refers to a northern direction, 90° refers to an eastern direction, and an orientation of − 90° refers to western direction. The orientation of the wrinkle ridge was automatically calculated by ArcGIS after projection. The detailed information of the wrinkle ridges’ orientations measured by the two methods is listed in Tables 3 and 4, respectively.

Fig. 4
figure 4

Example of orientation calculation of a wrinkle ridge. All the images are in the Mercator projection centred at 25°E, 28°N. a Orientation (α) of the wrinkle ridge measured by method O1. b Orientation (α) of the wrinkle ridge measured by method O2

Full size image
Table 3 Orientation measurement of wrinkle ridge by method O1
Full size table
Table 4 Orientation measurement of wrinkle ridge by method O2
Full size table

The orientations of the example wrinkle ridge measured by method O1and O2 are 6.49°, 7.71°, respectively, and the bias is 1.21°. However, considering the interpretation means of the wrinkle ridge and the shortcoming of the method used to measure the orientation of the wrinkle ridge, the discrepancy between these two methods is not very large and can be accepted to some extent. However, the effect of the accuracy of the central symmetry value calculation caused by orientation deviations will be discussed in Sect. 4.

3.2.3 Grid Size Determination

According to Eqs. (1) and (2), the result of the central symmetry value is not only related to the measurement accuracy of the orientation and length of the linear features but is also associated with the grid size that determines which will be used to calculate the central symmetry value in a study area. Thus, finding an appropriate or best grid size to calculate the central symmetry value of wrinkle ridges is very important.

In order to find the appropriate grid size, we used different grid sizes to investigate the influences of grid size on the results of the central symmetry values of the wrinkle ridges in Mare Serenitatis. Figure 5a shows three kinds of grid sizes: (1) a grid size (green rectangle with size of 530 km × 511 km) smaller than the range of Mare Serenitatis which cannot include all the wrinkle ridges in the study area, and should be used to calculate the central symmetry values; and (2) a grid size (red rectangle with size of 706 km × 682 km) determined according to the range of study area. In this paper, we adopted a minimum bounding envelope based on the scope of Mare Serenitatis to determine the grid size, and combined the boundary of Mare Serenitatis to ensure all useful wrinkle ridges were included to calculate the central symmetry value. (3) A grid size (purple rectangle with size of 855 km × 826 km) larger than the range of Mare Serenitatis, which not only includes all the wrinkle ridges in study area, but also contains some wrinkle ridges outside of study area, could also be used. In this case, the wrinkle ridges distributed outside of Mare Serenitatis are not useful but will make a profound impact on the accuracy of the calculated central symmetry values.

Fig. 5
figure 5

Grid size determination. a Three kinds of grid sizes for Mare Serenitatis. Black lines denote the wrinkle ridges distributed in Mare Serenitatis, the red lines denote the wrinkle ridges distributed outside of Mare Serenitatis. The boundary of Mare Serenitatis was downloaded from http://wms.lroc.asu.edu/lroc/view_rdr/SHAPEFILE_LUNAR_MARE. b Grid size for the four circular dominant ridge systems proposed by Maxwell et al. (1975)

Full size image

Apparently, if a grid size smaller or larger than the range of study area is applied to calculate the central symmetry value, the result may show a great error because the smaller grid size cannot include all the necessary wrinkle ridges while the larger grid size includes some useless wrinkle ridges. Thus, a grid size that matches the range of the study area can be considered an appropriate grid size. In this paper, we selected the minimum bounding envelope as an appropriate grid size to calculate the central symmetry value of the wrinkle ridges because it contains all useful wrinkle ridges that need to be involved in calculating the central symmetry value and can accurately reflect the distribution characteristics of wrinkle ridges.

4 Results and Discussion

4.1 Central Symmetry Value of Wrinkle Ridges

After calculating the length and orientation of wrinkle ridges via different methods mentioned above using the ArcGIS platform, a MATLAB© script was written and used to calculate the average orientation and central symmetry value of wrinkle ridges according to the Eqs. (1) and (2).

In this paper, we calculated the central symmetry values of the wrinkle ridges distributed in Mare Serenitatis (Fig. 5a) and those within four circular ridge systems (Fig. 5b) proposed by Maxwell et al. (1975). The related parameters and results are shown in Tables 5 and 6. Table 5 shows that the average orientations of wrinkle ridges in the whole Mare Serenitatis measured by methods O1 and O2 are − 11.54°, − 6.23°, respectively, and the bias is up to 5.31°. However, the bias of the central symmetry values is only 0.08. In Table 6, the larger bias of the average orientation of the four circular ridge systems comprising the ridge system reached 9.54°, however, the bias of the central symmetry value is only 0.04. Through analyzing these tables, we can see that the average orientations of wrinkle ridges measured by different methods may produce large discrepancies, but the central symmetry values calculated by the two methods do not cause very large biases, indicating that the value of central symmetry is dominated by both length and the orientation of the wrinkle ridges.

Table 5 Central symmetry value measurement of the wrinkle ridges for the whole Mare Serenitatis
Full size table
Table 6 Central symmetry value measurement of the wrinkle ridges in the four circular ridge systems
Full size table

According to a previous study (Liu 1985), the magnitude of the central symmetry value can be divided into different grades. When the central symmetry value is greater than 0.70, the distribution of the wrinkle ridges shows close to completely symmetry. When the central symmetry value is greater than 0.65, the distribution of wrinkle ridges has reached a high degree of central symmetry. For the ridge system of Mare Serenitatis, the central symmetry values of the wrinkle ridges are 0.59 and 0.51 when calculated by the two methods. For the four circular ridge systems, all the central symmetry values are in the range of 0.57–0.64, and the large deviation is 0.04. Because the value range of σ is between 0 and \({{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. \kern-0pt} 2}\left( { \approx 0.707} \right),\) the central symmetry values calculated for the whole Mare Serenitatis and within the four circular ridge systems show a medium degree of central symmetry.

4.2 Effect Factors of Central Symmetry Value

The equations and methods mentioned above show that the accuracy of the calculated central symmetry value is affected by the means of interpretation of the wrinkle ridges, the method used to measure the orientation and length of each wrinkle ridge, and the determined grid size used to calculate the central symmetry value of the study area. Thus, the result of the central symmetry value could be little different from that of this paper after improving the methods to interpret the wrinkle ridges, to measure the length and orientation of each wrinkle ridge and to determine the grid size.

In addition, because we only mapped the large scale wrinkle ridges in Mare Serenitatis due to limitations from the resolution of TC, there may exist incorrectly interpreted wrinkle ridges or missing wrinkle ridges which can also cause a discrepancy when calculating the central symmetry value.

4.3 Implications for the Formation of Wrinkle Ridges

The formation of wrinkle ridges is a very complex geological process and is currently considered to originate from tectonic processes (e.g., Plescia and Golombek 1986; Watters 1988; Ono et al. 2009). In our research, by calculating the central symmetry value of the wrinkle ridges in Mare Serenitatis, we found that the wrinkle ridges are uniformly distributed with a dominated orientation, and these results can reflect the degree of central symmetry of these features with a given magnitude. Although the formation mechanism of lunar wrinkle ridges is complicated, the distribution pattern, the average orientation and the central symmetry value can represent the direction of the stress field that formed these features. For Mare Serenitatis, the wrinkle ridges are distributed concentrically, which indicates that these features suffer stresses in different directions. However, the average orientation shows that there was a dominant stress direction among these features, and the central symmetry value can illustrate the degree of central symmetry of the wrinkle ridges that were formed by the stress.

5 Conclusion

To quantitatively analyze the distribution characteristic of wrinkle ridges, a parameter called the central symmetry value was introduced to analyze the degree of central symmetry of wrinkle ridges in lunar mares. This quantitative method can also be applied to those linear features that have concentric or radial orientations in other areas. Before applying this method to calculate the central symmetry values of wrinkle ridges, the length and orientation of each wrinkle ridge and the grid size must be determined. In this paper, we used two methods to measure the lengths and orientations of each wrinkle ridge and the corresponding study area, which is used to determine the grid size. Through calculating the central symmetry value of the wrinkle ridges in Mare Serenitatis and that of the four circular ridge systems, we found that the method can be applied to quantitatively analyze the degree of central symmetry of the linear features that were distributed in concentric or radial orientations, allowing a further understanding of the formation modes of wrinkle ridges. This approach can also be used to analyze the stress field that formed these features. However, the accuracy of this method is related to the measurement precision of the lengths and orientations of each linear feature as well as to the chosen grid size of study area. Thus, these factors need to take into account while calculating the central symmetry value.

In this paper, we made only a preliminary study of the central symmetry value of the wrinkle ridges in the lunar Mare Serentatis and that of the four circular ridge systems proposed by a previous study. In future works, we will study the central symmetry values of wrinkle ridges in other lunar mares or globally after refining the method to measure the length and orientation of each linear feature and to determine the grid size to derive a more accurate result than that of the present study. Furthermore, we will divide the central symmetry values into different grades to analyze the distribution patterns for the linear features across the whole lunar surface and to understand the global stress field of the Moon.