A Dissolved Gas Assessment Model for Power Transformers According to Weighted Association Rule Mining

Introduction

As one core part of power systems, power transformers are one key primary equipment, since their failure may cause power supply interruption and even blackouts which will result in significant economic losses. Ergo, it is vital to ensure the safe operation of power transformers. Any transformer failure may lead to the interruption of power supplies, which will consequently cause great losses (Cui et al., 2021; Zhang et al., 2021). Power transformers are usually affected by several inner factors such as thermal stress, overload, and aging of insulating materials. Therefore, the timely and effective fault diagnosis based on these internal characteristics of transformers will be salutary for the subsequent maintenance. Once the countermeasures are implemented, the potential risks of failure can thus be greatly reduced (Lijun et al., 2021; Meira et al., 2021).

Unlike the electrical signal parameters which are largely affected by the electromagnetic environment within the transformer, there is also a strong correlation between the fault event and the gas composition in transformer oil. Therefore, dissolved gas analysis (DGA) is commonly utilized for transformer fault diagnoses (Cui et al., 2020; Meira et al., 2021).

At present, many researchers have proposed a large number of research ideas on the DGA (Bakar et al., 2014), and considerable progress has been achieved. In the traditional methods, the three-ratio method, the Rogers ratio method, and the Duval triangle method based on the DGA have played an important role, but there are still some drawbacks such as the incomplete state coding and the absolutely coding boundaries. They might limit the practical application of these approaches (Malik and Mishra, 2016; Shi et al., 2016).

In recent years, many scholars have applied machine learning theories to transformer fault diagnosis modeling, and have achieved satisfying results. The first one is the DGA method based on the optimization algorithm (Asafuddoula et al., 2018). To improve the accuracy and reliability of oil-immersed transformer fault diagnosis, References (Youwen et al., 2021; Wu et al., 2021) studied a transformer fault diagnosis method based on genetic algorithm optimization of extreme gradient lifting, and Siada et al. employed fuzzy logic models to assess the concentration of each sort of the dissolved gas in (Abu Bakar and Abu- Siada, 2017), or to reduce the dependency for standardizing the DGA interpretation techniques by (Abu- Siada et al., 2013). In (Huanpeng et al., 2017), the Least Squares Dual Support Vector Machine (LS-TSVM) model was deployed. Based on the genetic algorithm, and Genetic Algorithm Support Vector Machine (GA-SVM) along with the crisscross optimization method for the DGA feature was realized in (Anbo et al., 2016; Jing et al., 2020). These DGA methods based on the optimization algorithm can often obtain the intuitive fault probability, but it is necessary to count the large-capacity data for a long period, which requires a larger size of input data.

The second type is the DGA method using the neural network (Jan and Verma, 2021). In (Yingjie and Tienan, 2021), a diagnosis method based on the improved Elman neural network was proposed. In order to improve the accuracy and performance under small sample data scenarios, a method based on the residual BP neural network was established in reference (Wenqing et al., 2020). In (Yan and Taihua, 2020), an optimized probabilistic neural network fault diagnosis method based on digital twinning technology was proposed. A transformer condition assessment method based on fuzzy neural network and local statistics was built in reference (Rigatos and Siano, 2016). The DGA method based on neural networks generally has strong stability and fault tolerance, but they also require large-capacity input data generally.

The third one is the DGA method based on the vector machine (Moazami et al., 2016). Reference (Yiyi et al., 2018) proposed a transformer fault diagnosis model based on the support vector machine (SVM) which was optimized by the imperial colonial competition algorithm, and Rao et al. selected non-linear SVM to classify diverse types of power transformer faults by (Rao et al., 2021). In (Jun et al., 2017), the AdaBoost algorithm was combined with the quadratic mapping support vector machine to find a transformer fault diagnosis model. References (Bacha et al., 2012; Xinbo et al., 2020) applied the support vector machine to realize the classification and discrimination of transformer faults. Although the results of the DGA method based on the vector machine are generally or close to the global optimization, it is difficult to solve the multi-classification problems.

To handle these, association rule mining (ARM) (Nahar et al., 2013) is often exploited in the DGA method because it can select input features or states according to requirements. In (Li et al., 2015), the diagnosis model is further optimized based on the grid search (GS) algorithm. An integrated algorithm combining the set pair analysis and the ARM was created by (Sheng et al., 2018). In (Tian -en et al., 2019), the probabilistic image model was applied in the ARM to further improve the efficiency. Remarkable achievements have been made in the literature, whereas there are still some improvable aspects. Firstly, the standard ARM algorithms usually deploy a fixed and uniform importance measure criterion, thus some components with a lower frequency of occurrence will be directly screened out without any assessment. However, there might also be some high-impact (HI) components that can cause failures in these low-probability components, hence these high-risk- low-probability (HILP) components should be extracted and analyzed; Secondly, the risk weight of the selected HI components ought to be determined directly by the risks they generate, rather than simply via their frequency of occurrence; Finally, the predefined parameters in the ARM need to be adjusted or modified during the diagnosis to further enhance the performance.

To realize these, this paper proposes a DGA method based on an improved Weighted Association Rule Mining (WARM) model. In the preprocessing step, the assessment mapping space is established for collecting and integrating all the input data. In this model, the first step is to explore the risky components from the whole input components. The calculation methods of several significance selecting criteria are modified to pick out the HILP components, so that the HILP data can be extracted from the rare data for further analysis along with the HI components which are chosen from the common components. The second step is to evaluate the risk level of the distinguished risky components from the first step, and a risk weight evaluation approach is proposed in light of the component importance measure (CIM). In this model, the influence degree of the HI and the HILP components themselves on the variation level of total reliability of a transformer, rather than the proportion in a database or the frequency of appearance, is incorporated to measure the risk weights. At last, a dynamic adjustment framework is established where the parameters in the risk weight evaluation approach can be periodically adapted and amended in line with the previous diagnosis performance. An empirical case study is conducted, and the results demonstrate that the proposed method can improve diagnostic accuracy, operational efficiency, and reliability during real-world applications.

Data Preprocessing

In order to construct a unified processing space for subsequent analysis, the whole collected fault event records, as well as the relevant features and including components need to be integrated.

Suppose $\left\{t_A,t_1,t_2,\dots t_i,\dots ,t_m\right\}$ is a vector contains the labels of totally $m$ fault records, where $t_i$ is one fault event while $t_A$ is the label number. Assuming that $A=\{a_1,a_2,\dots ,a_j,\dots ,a_n,a_T\}$ is a vector containing all $n$ features in the database, where $a_j$ ($j=1, 2, \dots , n$) is one feature, and $a_T$ is the target feature. For a feature $a_j$, supposing $a_j=\left\{e_{j,1},e_{j,2},\dots ,e_{j,k},\dots ,e_{j,l}\right\}$ is a vector of all the $l$ elements contained, where $e_{j,k}$ ($k=1, 2, \dots ,l$) is one element of the feature $a_j$. This paper selects $X=\left\{x_{i1},x_{i2},\dots ,x_{ij},\dots ,x_{in}\right\}$ as the whole relevant factors in a fault event $t_i$, where $x_{i,j}$ can be any one component of the feature $a_j$. Seven commonly applied types of dissolved gases in transformer oil as inputs, including the contents of hydrogen (H₂), methane (CH₄), acetylene (C₂H₂), ethylene (C₂H₄), ethane (C₂H₆), the relative gas production rates of carbon monoxide (CO) and carbon dioxide (CO₂) (Rezaie et al., 2022) are considered in this paper as the input features.

As for the target feature $a_T$, the states of a transformer are selected as the components of the target, and assumes $T=\{T_1,T_2,\dots ,T_o,\dots ,T_m\}$ is a vector that includes the target features in all fault event records. In this paper, seven states of one transformer are taken into account: normal operation, low temperature overheating, medium temperature overheating, high temperature overheating, low energy discharge, high energy discharge, and partial discharge. Hence, $T_o$ may belong to any one of all the seven states, that is $T_o=T\left(\beta \right)\in \left\{T\left(g_1\right),T\left(g_2\right),\dots ,T\left(g_7\right)\right\}$. Combined with the supposition of the factor set $X$, an association rule or more specifically, the component-risk patterns can be delineated as $X\to T$

Based on the above assumptions, the assessment mapping space can be constructed as a matrix form $\mathit{H}$:

where each row (except the first row) indicates one record of a fault event, $x_{ij}$ is an entry in the $i$ -th fault record, that is, any one element $e_{j,k}$ corresponding to feature $a_j$. Thus, in an event $t_i$, $x_{i,1},x_{i,2},\dots ,x_{i,j},\dots ,x_{i,n}$ are the corresponding components in each feature, $T_i$ is the result.

WARM Model

Background of ARM

Assuming that there is a set $I$ containing all items, a subset $X$ of $I$ is called the item set. Supposing the database $D=\left\{t_1,t_2,\dots ,t_m\right\}$ contains all the fault records. An association rule can be expressed as $X\to T$, which means that if the item set $X$ appears, the target $T$ will also occur.

The establishment of association rules generally depends on the discovery of the large item sets as well as the frequent rules, and the selection criteria for them are called the significance selecting criteria. The most commonly-used significance selecting criterion is called the support $\left(supp\left(X\right)\right)$, which describes the proportion of $X$ in $D$ (Hipp et al., 2000). In addition, there are some evaluation criteria focusing on the selection of frequent rules. The confidence ($conf(X\to T)$) refers to the proportion of $X$ that contains $T$ simultaneously (Doostan and Chowdhury, 2017); The rule power factor $\left(rbf\left(X\to T\right)\right)$ measures the weight of confidence by $X\to T$ (Hipp et al., 2000); The certainty factor $\left(cf\left(X\to T\right)\right)$ measures the change degree of the probability of $T$ appearing simultaneously in the rules containing $X$ (Ochin et al., 2016). Based on the aforementioned criteria, if the score of the item sets or rules can meet or above the corresponding thresholds, these item sets and rules will be considered as the large item sets and frequent rules.

Refinement of Significance Selecting Criteria

Among the input components, there are often some that occur less frequently. However, a part of these rare feature quantity values will also lead to transformer failures, then cause serious losses. Therefore, those HILP components cannot be simply ignored. The standard ARM algorithm employs the same and fixed score calculation methods of significance selecting criteria, which makes the rare variables be discarded directly without any analyses. Therefore, based on the standard significance selecting criteria, this paper designs the weighted significance selecting criteria that consider the rare variables.

In the ARM, large item sets and frequent rules are filtered by a uniform calculation approach which results in the dominance of common components that account for a large proportion of the database. In other words, rare components along with the HILP components will be screened out. In order to properly handle these rare data, this paper establishes four weighted significance selecting criteria.

Firstly, an association rule can be redefined as:

where $X^{\text{f}}$ and $X^{\text{r}}$ represent the item sets containing common components and rare components, respectively.

If the association rule contains at least one rare element in a feature $a_j$, the weighted significance selecting criteria can be built as:

where ${\mathbf{G}}^{1\times n}=\mathit{H}\left(i,2\sim \left(n+1\right)\right)$; $|\cdot |$ represents the cardinality of the fault event records that meet all the inside conditions; $T\left(\beta \right)$ denotes the states under study. For the confidence, rule power factor, and certainty factor, the superscript $\beta$ shows that there are seven different forms of these criteria corresponding to seven different transformer states.

Establishment of Risk Weight Evaluation Model

Since different components in each feature have different impacts on the states of a transformer, further investigation of the relative magnitude of the risk weight of each component is indispensable. In most current studies, the evaluation of risk weights relies on the proportion in a database or the frequency of occurrence. However, they are not equal to the influence of a component on the state of the entire transformer. Therefore, the relative risk weights of each component are determined based on the degree of influence on the transformer itself in this paper.

This paper describes the overall fault risk of a transformer based on the system risk structure theory, and the principle of the CIM is utilized to describe the impact of different components, so as to design the risk weight evaluation model. For the purpose of distinguishing the relative risk weights of rare components, this paper forms two independent processing subspaces of $\mathit{H}$: $S^{\text{f}}$ contains all the records, while $S_j^{\text{r}}$ only includes the records of either rare component in a certain feature $a_j$. In addition, $a_j^{\text{f}}$ and $a_j^{\text{r}}$ represent all the common and rare components in that feature, respectively.

The CIM can measure the impact of each component on the overall risks. In this paper, the risk of a component, that is, the risk of an element $e_{j,k}$, means that a fault event is related to that element $e_{j,k}$ in a feature $a_j$. The overall risk of a transformer indicates the comprehensive likelihood of a failure in that transformer. This paper deploys two CIM indicators. The risk achievement worth (RAW) (Vesely et al., 1983) describes the relative rise in the overall risk due to the presence of elements $e_{j,k}$ , and its mathematical expression is:

where $1-R\left(0_k,\text{p}\right)$ denotes the overall risk when the element $e_{j,k}$ is confirmed to be related; $1-R\left(\text{p}\right)$ represents the overall risk.

Similarly, the risk reduction worth (RRW) (Vesely et al., 1983) represents the relative decline in the overall risk if the element $e_{j,k}$ does not appear, and its mathematical expression is:

where $1-R\left(1_k,\text{p}\right)$ denotes the overall risk when the element $e_{j,k}$ is ensured to be irrelevant.

In a fault record, even if a component changes, this fault may no longer occur. Ergo, the occurrence of the fault requires that all the corresponding elements of each feature in this record are confirmed to be relevant. Based on this, the mathematical form of the overall risk can be written as:

In this paper, the relative risk weight of an element $e_{j,k}$ is composed of two parts, which can be expressed as:

where ${\text{ω}}_{j,k}^{\text{f}}$ represents the risk caused by common elements, ${\text{ω}}_{\text{j},\text{k}}^{\text{r}}$ represents the risk from rare elements.

The mathematical expression of ${\text{ω}}_{j,k}^{\text{f}}$ is:

This paper selects the mean value of the impact of formula (7-8) to measure the risk from rare elements, so ${\omega }_{j,k}^{\text{r}}$ can be expressed as:

where $A_{\text{RAW}}$ and $A_{\text{RRW}}$ illustrates the risks from the risk increase and the risk decrease, respectively, and namely:

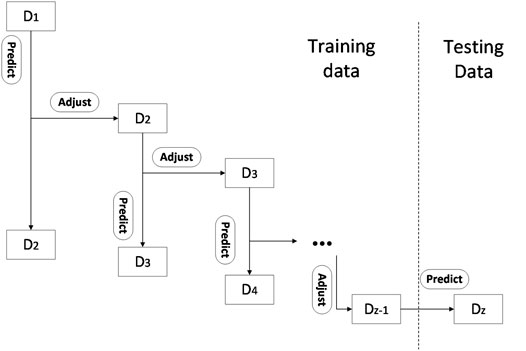
Formation of Adjustment Framework

During the application of the diagnosis method, the occurrence of failures varies in different periods. Moreover, with the increase in application time, the parameters ought to be adjusted according to the previous performance to further improve the accuracy of weight evaluations.

In this paper, 1 year is supposed as a research cycle. Therefore, let $D_y\in D=\left\{D_1,D_2,\cdots ,D_y,\cdots ,D_{\text{Z}}\right\}$ denote the records of 1 year in the database $D$, that is, the records of all faults within that year. Thus, the parameters in the model will be dynamically modified per year, which is shown in Figure 1.

FIGURE 1. An illustration of dynamic parameter adjustment framework.

To start with, the initial parameters can be determined from the previous knowledge or engineering experiences. Next, the parameters will be amended in line with the diagnosis performance of the previous cycle. If the actual number of faults in the investigated system is higher than the predicted number of faults according to the comparison between the predicted results and the actual consequences at the end of a year $y$. In this case, the model needs to “identify” more faults in the next period $y+1$, i.e., the thresholds of significance selecting criteria should be reduced. Therefore, the threshold needs to be adjusted downward compared to their foregoing values in $y$. On the contrary, when the actual number of faults is less than the predicted numbers, the thresholds need to be updated upward. In summary, the dynamic adjustment of the method is achieved by resetting the threshold of the significance selecting criteria. Also, the importance scores solved by the weighted criteria calculation method are updated directly in accordance with the new annual database $D_{y+1}$. By combining these two, the proposed approach can be updated based on the rules via the different years of input data.

Empirical Case Study

Database

In this case study, the transformer maintenance records from a high-voltage transmission system in a central province of China are selected as input data. The total number of sample records is 1,564 which covers the contents of five gases (H₂, CH₄, C₂H₂, C₂H₄, C₂H₆) and relative gas production rates of two (CO, CO₂). Seven states of a transformer (normal operation, low temperature overheating, medium temperature overheating, high temperature overheating, low energy discharge, high energy discharge, and partial discharge) are incorporated as the target.

Validation Tools

In this paper, two 10-fold cross-validation test cases are generated: the general case which is conducted separately according to all states of a transformer; the state case that studies the individual influence of the events by each kind of the state.

When comparing the diagnosis results with the test data, the receiver operating characteristic (ROC) and the precision-recall (PR) curves are deployed to validate the performance (Ziege, 2012). On the basis of these two curves, the area under the curve (AUC) (Swets, 2016) is implemented as the performance indicator, and the higher the AUC value is, the more accurate the diagnosis will be.

General Case

In the very beginning, this paper takes all types of transformer faults as a whole, and applies the WARM-based DGA method to diagnose whether the transformer is faulty or not, i.e., the transformer has only two states: faulty and normal operation.

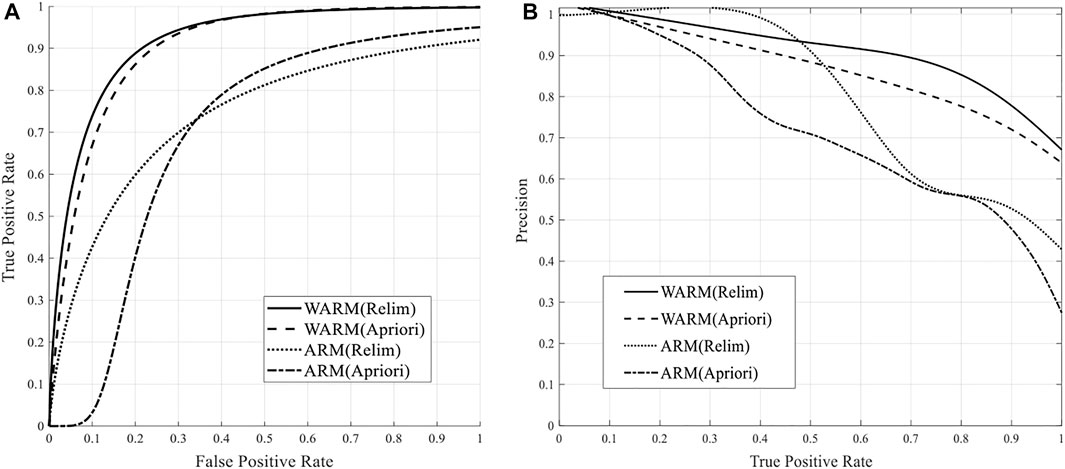
To verify the effectiveness of both the significance selecting and risk weight evaluation enhancements in the proposed WARM model, two standard ARM algorithms are taken for comparison: the Relim and the Apriori methods. These two algorithms are different in item searching, recording, and sorting, whereas sharing similar procedures in significance selecting and weight evaluation steps. In that case, two DGA techniques (WARM(Relim), WARM(Apriori)) that adopt the improved significance selecting criteria and risk weight evaluation model but apply the Relim and the Apriori algorithms, respectively, will be compared with the two standard forms (WARM(Relim), ARM(Apriori)). The comparison of the ROC and PR curves of these DGA methods are shown in Figure 2.

FIGURE 2. Performance comparison of general case: (A) ROC, (B) PR.

It can be concluded from Figure 2 that the WARM method which is based on the refined significance selecting criteria and risk weight evaluation model can achieve more accurate transformer fault diagnoses than the ARM model. It can be concluded that the accuracy of the results obtained by the Relim and the Apriori algorithms is relatively close. That is, these two algorithms cannot notably improve the diagnosis precision compared with each other. However, compared with the DGA method based on the ARM, the AUC of the ROC and PR curves of both two algorithms with the WARM model is raised by 19.6 and 14.1% on average. This indicates that the proposed WARM model can successfully enhance the diagnostic performance for either one of the two algorithms.

State Case

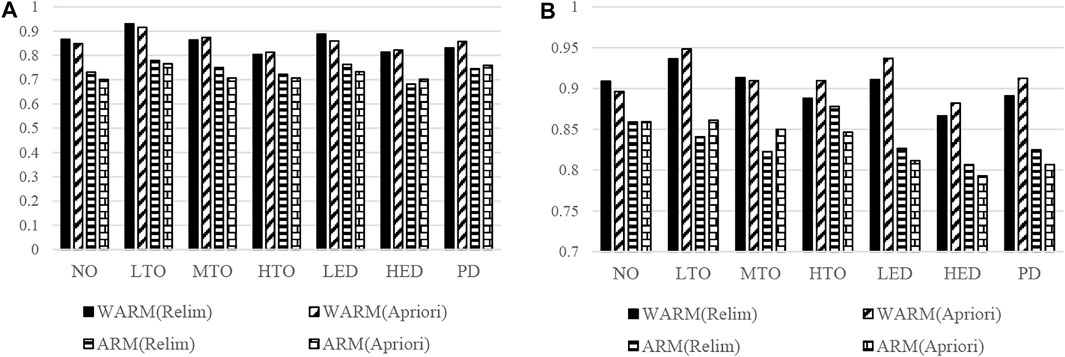
Next, the separate diagnoses of all the seven states are carried out, and the comparison is illustrated in Figure 3, where NO-normal operation, LTO-low temperature overheating, MTO-medium temperature overheating, HTO-high temperature overheating, LED-low energy discharge, HED-high energy discharge, and PD-partial discharge are applied.

FIGURE 3. Performance comparison of state case by AUC statistics: (A) ROC, (B) PR.

From Figure 3, the enhancements in diagnoses performance can be achieved via the significance selecting and risk weight evaluation in the WARM model for all the seven transformer conditions. Among them, the diagnosis of the LTO is the most precise one whereas the HED gets the lowest scores in both two evaluations. According to the input database, the HED events seldom happen in recent years while the LTO is one most frequent events. This is in line with the different data volumes of each transformer state, so as the performance. Nevertheless, the significant enhancement of the HED is conducted through the WARM model. Ergo, the benefits of the WARM can be verified especially when the input data is limited. Furthermore, the WARM-based method is also able to operate during some extreme scenarios.

Conclusion

For the purpose of handling some limitations in the standard ARM-based DGA method, such as ignorance of the HILP data, the simple evaluation of risk, and the static parameters during applications, this paper proposes an enhanced WARM-based DGA technique. The main works can be summarized as:

1) In the first step, the risky components ought to be distinguished from the whole input data. Unlike the common components, the rarely distributed components are generally viewed as trivial components and simply discarded. Nonetheless, some HILP components which may also cause fault events should be extracted from the rare components. To this end, the calculation approach of four significance selecting criteria is rebuilt, and the records with any rare component of each feature will be explored once again to decide the HILP components according to the different distributions of rare components in every feature. This can improve the diagnostic accuracy and cover some potential extreme situations during applications;

2) In the second step, the risk level of each risky component will be assessed. In real scenarios, the correlation between a component and the fault event risk is not simply equal to its percentage in the database or frequency of occurrence. That is, a frequent component may not be a risky one whereas a rare component might be a risky one. Ergo, based on CIM, the risk weight of each extracted HI or HILP component can be measured straightforwardly according to the corresponding impact on the variation direction and amounts of the overall risks of a transformer, rather than simply by the frequency of appearance or the data share;

3) During applications, the predefined default parameters might not be suitable or optimal within different scenes or periods. In this paper, these parameters will be modified or adapted in accordance with the previous diagnostic performance, and can thus further improve the accuracy, especially within dissimilar conditions in future periods.

The results of an empirical study validate that the proposed DGA method can ameliorate the precision, practicability, and efficiency within real scenarios.

Data Availability Statement

The datasets presented in this article are not readily available because secrecy agreement. Requests to access the datasets should be directed to State Grid of China.

Author Contributions

CS: Conceptualization, Methodology, Software, Writing; ZZ: Data curation; YZ: Investigation; ZJ: Supervision; JH: Validation; CH: Reviewing.

Funding

This work is financially supported by Key Laboratory of Renewable Energy Electric-Technology of Hunan Province, Grant No: 2020ZNDL006.

Conflict of Interest

Author CH is employed by the Northeast Branch of State Grid Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References