Inline holography of miniaturized objects with an intrinsic reference angle determined by the sagitta

Abstract

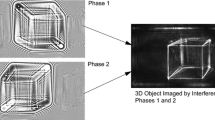
The twin image problem, well known in Gabor holography, greatly obstructs the output of high-quality holograms. Previous solutions include numerical and instrumental means to eliminate or mitigate the issue. The proposed method demonstrates the feasibility of using the sagitta angle in a spherical reference beam as an intrinsic reference angle within in-line holography. Along with a miniaturized version of the object, to allow for a wide range of object sizes, from millimeters to meters, with a small variation within the original optical system. The inherent reference angle allows for a separation of the twin images in the reconstruction of a Gabor hologram, while maintaining the system on axis. Under lens-less Fourier criteria, the peripheral information of the visual field interferes with a spherical wave to generate an interference pattern that results in a hologram with separated images.

Appendices

Appendix A Flat reference waves

The use of plane waves does not meet the Fourier criterion without lenses, since the distance z of the object at a given position does not correspond to z of the plane waves. Plane waves derived from the algebra of the cosines directors, by construction z has very large values, to induce that the wave face is constant.

Fig. 9

shows the holograms with plane reference wave, a center, b shifted 100 pixels, c shifted 200 pixels, d shifted 300 pixels. e–h show the holograms of the figures above. Portrait courtesy of the Smithsonian Libraries and Archives [14]

The second row of Fig. 9 shows the holograms of the objects in the first row, using as reference beam a plane wave, where it is clearly observed that there is no spatial fringe modulation to separate the superposition of the conjugate pair of images with a shift. Figure 9a shows the characteristic Gabor-like hologram, in the following figures (b), (c), and (d), the pattern is identical to (a), but shifted. This result is as expected, since there is no sagitta.

Fig. 10

a object, b hologram, c reconstruction with FFT

Figure 10a shows the object of 256 gray levels, displaced by 100 pixels. Fig. 10b displays a hologram generated with plane wave, which is later reconstructed in 10c using the FFT algorithm and applying the logarithm function, to amplify the visualization; where it is observed that it is not possible to reconstruct it by this way. The only way to extract the information is by reconstructing plane by plane with the Huygens–Fresnel–Kirchhoff equation to obtain the image, which will be modulated by the zero order, the halo, and the conjugate pair information.

Appendix B Field of view analysis

The Newton’s rings in Fig. 11 were captured by the CCD sensor by substituting the object with a plane mirror at a $90^{\circ }$ angle, overlapping with the spherical reference beam in the CBS. Newton’s rings appear because of the difference in radii of the two, since the spherical waves emerge at different distances from the microscope objectives [13]. The appearance of Newton’s rings further support the notion that the full system is aligned with the optical axis.

Fig. 11

a Shows the Newton rings obtained by a reference spherical wave and spherical calibration wave. b Detail of the rings in the upper left corner of a

Table 1 shows the change of the ring frequency (f) when influenced by the radius of curvature of the reference spherical wave (r) varying from 300mm to 165mm. As previously mentioned, the CCD has a pixel size (ps) of $4.29\mu m$, and the photo sensor can resolve the fringes caused by the sagitta as long as the condition $ps<p$ is satisfied. The period (p) of the rings decreases as one moves away from the center of the photo sensor. The working wavelength was $632.8x10^{-6}mm$ and the L chord was taken as the maximum diagonal of the sensor $L=26.82mm$

Table 1 Analysis of the resolvability of the FOV

For each r there is a number of rings over the sensor area. We calculated the radius of the nth ring, the periods, and the frequencies as described in Eqs.5 and 6. The sagitta (S) from Eq. 4 was also included to visualize the phase delay of the spherical wave at the edges of the photo sensor. The data in bold indicates that parts of the CCD will not be able to resolve the interference fringes produced by the sagitta. The rest of the data corresponds to an r suitable for working in any part of the sensor area.