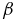ABSTRACT
We study the nonlocal nonlinear coupling and generation of kinetic Alfvén waves (KAWs) and kinetic slow waves (KSWs) by magnetohydrodynamic Alfvén waves (MHD AWs) in conditions typical for the solar wind in the inner heliosphere. This cross-scale process provides an alternative to the turbulent energy cascade passing through many intermediate scales. The nonlinearities we study are proportional to the scalar products of wave vectors and hence are called "scalar" ones. Despite the strong Landau damping of kinetic waves, we found fast growing KAWs and KSWs at perpendicular wavelengths close to the ion gyroradius. Using the parametric decay formalism, we investigate two independent decay channels for the pump AW: forward decay (involving co-propagating product waves) and backward decay (involving counter-propagating product waves). The growth rate of the forward decay is typically 0.05 but can exceed 0.1 of the pump wave frequency. The resulting spectral transport is nonlocal and anisotropic, sharply increasing perpendicular wavenumbers but not parallel ones. AWs and KAWs propagating against the pump AW grow with about the same rate and contribute to the sunward wave flux in the solar wind. Our results suggest that the nonlocal decay of MHD AWs into KAWs and KSWs is a robust mechanism for the cross-scale spectral transport of the wave energy from MHD to dissipative kinetic scales in the solar wind and similar media.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Magnetohydrodynamic Alfvén waves (MHD AWs) permeate the solar atmosphere and the solar wind (Belcher & Davis 1971; Mathioudarks et al. 2012). These waves are thought to be produced by the convective motion jostling magnetic flux tubes below the photosphere and/or by the magnetic reconnections in the photospheric network (Ruzmaikin et al. 1998; Ryutova et al. 2001; Cranmer & van Ballegooijen 2005). There is ample observational evidence for MHD AWs in the chromosphere (De Pontieu et al. 2007; Cirtain et al. 2007; He et al. 2009; McIntosh et al. 2011), corona (Tomczyk et al. 2007; Okamoto et al. 2007; Tomczyk & McIntosh 2009), and solar wind (Belcher & Davis 1971). Recent observations of the transition region and solar corona have revealed a significant energy flux carried by the ubiquitous outward-propagating AWs, which is more than enough to heat the solar corona and to accelerate the fast solar wind (McIntosh et al. 2011). These waves are also thought to accelerate the slow solar winds and power the solar wind turbulence (Cranmer et al. 2007). However, how MHD AWs dissipate and deposit energy in the plasma of solar atmosphere and solar wind remains unresolved.
The inhomogeneous plasma density and flow in the solar atmosphere and solar wind support the phase mixing and resonance absorption of MHD AWs (Ionson 1978; Heyvaerts & Priest 1983; Voitenko & Goossens 2006), which evolve to small-scale kinetic Alfvén waves (KAWs) undergoing an efficient dissipation. The small dissipative AW scales can also be generated through the turbulent cascade mechanism in the AW turbulence resulting from nonlinear local interactions among counter-propagating AWs (Matthaeus et al. 1999; Cranmer & van Ballegooijen 2003; Verdini & Velli 2007; van Ballegooijen et al. 2011). Modern theory of the AW turbulence suggests that KAWs are generated by the turbulent cascade at kinetic ion or electron scales (Howes et al. 2008, 2011; Voitenko & De Keyser 2011; Zhao et al. 2013), which is consistent with the turbulence characteristics measured in situ in the foreshock of the Earth and in the quiet solar wind (Sahraoui et al. 2009; Alexandrova et al. 2009). There is growing evidence that the proton kinetic scales (He et al. 2012; Roberts et al. 2013), as well as shorter ones (Chen et al. 2013), are dominated by KAWs (see also the overview of some measured KAW effects by Podesta 2013). Kinetic-wave–particle interactions of KAWs are efficient even in weakly collisional plasmas and in plasma heating and particle acceleration. These phenomena can be responsible for energy deposition by AWs in the solar atmosphere and solar wind (Cranmer & van Ballegooijen 2003; Wu & Fang 2003; Wu & Yang 2007; Chandran et al. 2010).
The above-mentioned processes imply a gradual evolution of wave energy from large MHD to small kinetic scales. At the same time, recent theory (Voitenko & Goossens 2005; Zhao et al. 2011a, 2011b) and simulations (Singh & Rao 2012) suggest that MHD waves can couple energy directly into small-scale kinetic waves. The first nonlocal decay of MHD-scale fast mode wave into KAWs was considered by Voitenko & Goossens (2002). Later, Voitenko & Goossens (2005) demonstrated analytically that the nonlocal decay of MHD AWs into KAWs should occur in very low-β plasmas where the gas/magnetic pressure ratio is less than the electron/proton mass ratio, β < me/mi. This result was recently confirmed by numerical simulations (Singh & Rao 2012). A similar process, incorporating an oblique MHD AW as the pump wave, has been considered (Zhao et al. 2011a), and a fusion interaction between MHD AWs and KAWs has been studied in the low-β domain me/mi ≪ β ≪ 1 (Zhao et al. 2011b). The advantage of the nonlocal decays as the spectral transport mechanisms is that they transport energy in a single step across a wide interval of scales, avoiding many short local steps as, for example, in the local turbulence cascade (Howes et al. 2008; Zhao et al. 2013). Therefore, the nonlocal decays can provide faster spectral transport than the turbulence cascade or other gradual processes.
Formalism of parametric decay instability was first invented by Oraevsky & Sagdeev (1962) for electrostatic waves, which was then extended by Galeev & Oraevskii (1963) for electromagnetic MHD AWs. In the low-β plasma the strongest MHD decay (where all participating waves are MHD waves) was found into the backward propagating AW and forward slow wave (SW). The corresponding growth rate by Galeev & Oraevskii, γGO, can be estimated as

where ω and B are the pump AW frequency and magnetic amplitude, respectively.
The process of the AW decay into the backward AW and forward SW has been confirmed by many subsequent analytical and simulation studies with various modifications (see recent papers by Nariyuki & Hada 2006; Matteini et al. 2010; Verscharen et al. 2012; Gao et al. 2013, Gao et al. 2014). The parametric decay is found in the hybrid simulations for both parallel and oblique AWs (Matteini et al. 2010; Verscharen et al. 2012; Gao et al. 2013, Gao et al. 2014), and AWs decay rapidly as the beam-induced oblique KAWs appear (Nariyuki et al. 2012). Simulations by Matteini et al. (2010) have shown that the ions can be accelerated by the magnetic-field-aligned electric field of the product SWs and can form the ion beams.
In the present paper, we keep leading-order nonlinear terms proportional to the scalar product (k0⊥ · k1⊥) of the pump and product wave vectors k0⊥ and k1⊥. These terms are responsible for the so-called "scalar" nonlinear interaction. In terms of the pump wave magnetic field B these terms are proportional to 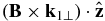 . The relevant nonlinear equations describing the scalar nonlinear interaction are derived below (Equations (26) and (27)). Some of these nonlinear terms, not accounted for in previous analytical studies, allowed us to capture a nonlocal MHD/kinetic decay of MHD AWs into kinetic-scale AWs and SWs. We show that in the low-β plasmas the MHD AWs can effectively excite KAWs and kinetic slow waves (KSWs) at small kinetic scales of about ion gyroradius ρi. In some cases, the MHD/kinetic decay can be more efficient than the MHD/MHD decay by Galeev & Oraevskii (1963) and generate dissipative KAWs and KSWs thus providing plasma heating and decreasing MHD AW amplitudes in the solar corona and solar wind. For example, it may contribute to the observed decrease of the wave amplitudes as the waves propagate from 1.1 R☉ to 1.4 R☉ in polar coronal holes (Bemporad & Abbo 2012; Hahn et al. 2012), and to KAW and KSW spectra observed in the solar wind turbulence (Howes et al. 2012; Klein et al. 2012) and in the terrestrial auroral zones (Wygant et al. 2002).
. The relevant nonlinear equations describing the scalar nonlinear interaction are derived below (Equations (26) and (27)). Some of these nonlinear terms, not accounted for in previous analytical studies, allowed us to capture a nonlocal MHD/kinetic decay of MHD AWs into kinetic-scale AWs and SWs. We show that in the low-β plasmas the MHD AWs can effectively excite KAWs and kinetic slow waves (KSWs) at small kinetic scales of about ion gyroradius ρi. In some cases, the MHD/kinetic decay can be more efficient than the MHD/MHD decay by Galeev & Oraevskii (1963) and generate dissipative KAWs and KSWs thus providing plasma heating and decreasing MHD AW amplitudes in the solar corona and solar wind. For example, it may contribute to the observed decrease of the wave amplitudes as the waves propagate from 1.1 R☉ to 1.4 R☉ in polar coronal holes (Bemporad & Abbo 2012; Hahn et al. 2012), and to KAW and KSW spectra observed in the solar wind turbulence (Howes et al. 2012; Klein et al. 2012) and in the terrestrial auroral zones (Wygant et al. 2002).
The outline of the paper is as follows. Section 2 presents a detailed derivation for the nonlinear coupling among low-frequency waves in the two-fluid plasma model. We then obtain the growth rate for KAWs and KSWs participating in the nonlinear decay MHD AW = KAW+KSW, where KAW can propagate either in the same direction as MHD AW or against it. In Section 3, a preliminary analysis is presented for these two decay channels in the non-dissipative case. It is shown that KAWs propagating against the MHD AW are generated at about the same rate as the co-propagating KAWs. We further describe the model for the collisionless dissipation of KAWs and KSWs in Section 4, and investigate the nonlinear decay of MHD AWs into dissipative KAWs and KSWs in Section 5. In Section 6, we discuss our results in comparison to other studies, and present our conclusions in the final section, stressing the importance of the studied decay for the nonlocal spectral transport from MHD to kinetic scales in the solar wind.
2. TWO-FLUID MODEL
We start from the basic two-fluid and Maxwell equations, expanding all variables into the sum of background part plus perturbation: A0 + A. Then the equations for the perturbations are
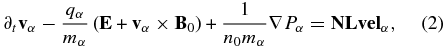
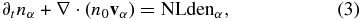


where we account for the nonlinear terms:
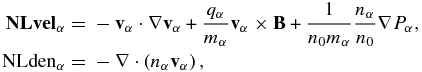
and vα, nα, E, B, and J are perturbations of the plasma velocity, number density, electric field, magnetic field, and current density, respectively; qα, mα, Tα, and Pα = Tα(n0 + nα)γ are particle charge, mass, temperature, and thermal pressure, respectively, for particle species α, i.e., α = i for the ions and α = e for the electrons; n0 and B0 are the background number density and magnetic field, respectively.
2.1. Derivation of General Nonlinear Equation
From the momentum equation (Equation (2)), the fluid velocity perturbation for the low-frequency waves where the wave frequency is much smaller than the ion cyclotron frequency can be expressed as
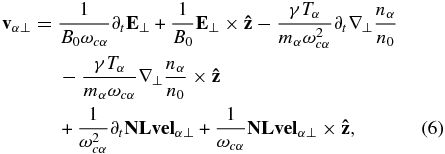
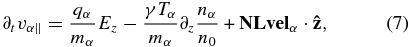
where ωcα ≡ qαB0/mα is the particle cyclotron frequency, and subscripts "∥" and "⊥" represent the perturbation parallel and perpendicular to the direction of the background magnetic field  .
.
By substituting Equations (6) and (7) into the following expression of the current density,
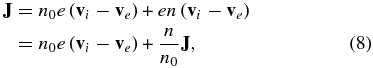
we obtain the perpendicular and parallel currents as
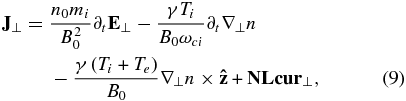
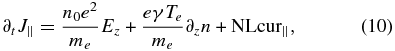
with the nonlinear terms
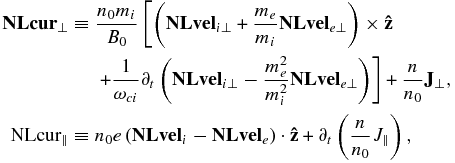
where the quasi-neutral condition has been used, ni = ne ≡ n. The same currents can also be expressed in terms of the electric field from Equations (3) and (4):
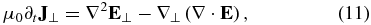
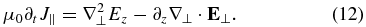
By combining Equations (9)–(12), we get the coupled equations for electric field components:
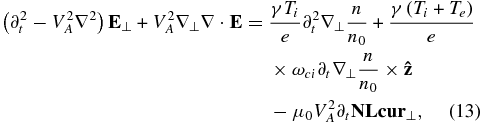
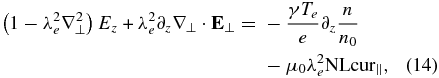
where VA is the Alfvén speed and λe is the electron inertial length.
It is convenient to define a local coordinate system with three orthogonal unit vectors  ,
, 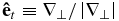 , and
, and 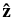 . The corresponding electric field components Ep Et and Ez can be expressed in terms of the normalized density perturbation n/n0:
. The corresponding electric field components Ep Et and Ez can be expressed in terms of the normalized density perturbation n/n0:
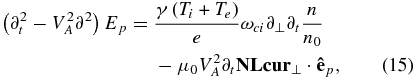
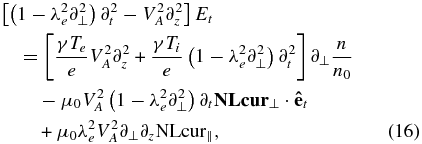
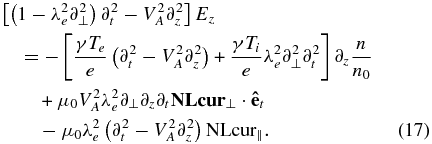
The fourth complementing equation connecting n/n0 to Ep, Et, and Ez is derived from Equations (3), (6), and (7):
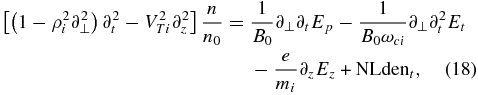
where ρi = (VTi/ωci)1/2 is the ion gyroradius, VTi and TTe are, respectively, the ion and electron thermal velocities, and the nonlinear term is defined as
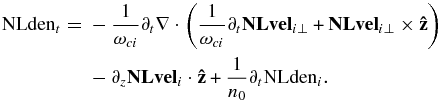
Using Equations (15)–(17), we can eliminate from Equation (18) all three components of the electric field, thus arriving to the general nonlinear equation for the low-frequency wave coupling in terms of n/n0:
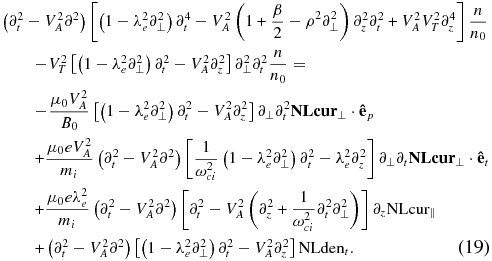
The definitions here are as follows:
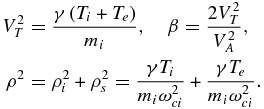
2.2. Linear and Nonlinear Responses of KAWs and KSWs in the Intermediate- Plasmas
Plasmas
The general nonlinear equation (Equation (19)) describes the nonlinear dynamics of low-frequency wave modes: fast, slow, and Alfvén. In a specific plasma environment and for particular wave modes, the expression (Equation (19)) can be significantly simplified. Here we consider the nonlinear evolution of two plane waves, KAW1 and KSW2, with amplitudes ∝exp (ik1, 2· r − iω1, 2t) in the low-β plasmas where both these waves are highly oblique, k⊥ ≫ kz. The wave properties of these two modes have previously been discussed in detail (see, e.g., Chen & Wu 2011a, 2011b, and references therein). The fast wave decouples in this case and we retain only KAWs and KSWs.
Let us first consider the nonlinear equation (Equation (19)) for KAWs with ω∝VAkz. After the small terms of the order of 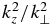 and
and 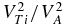 are neglected, the nonlinear equation reduces to
are neglected, the nonlinear equation reduces to
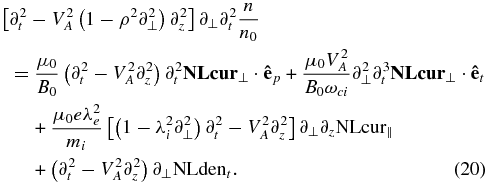
If we discard the nonlinear terms on the right-hand side of the last equation, the linear dispersion relation of KAWs is obtained:
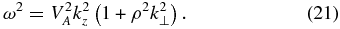
Then we can derive explicit expressions for the linear KAW response:
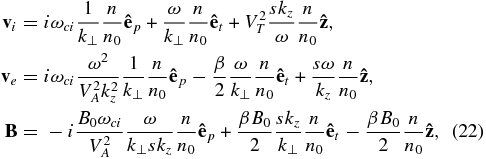
where s = kz/|kz| denotes the propagation direction of the wave, such that s = 1 for the wave propagating in the direction of B0, and s = −1 for the waves propagating against B0.
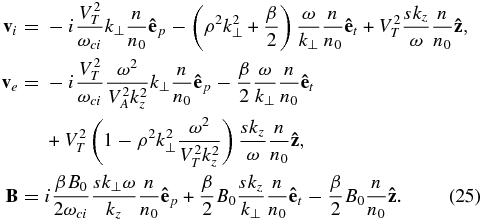
For KSWs with ω∝VTkz, the nonlinear equation (Equation (19)) reduces to
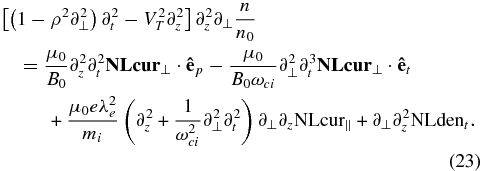
Hence the linear dispersion relation for KSWs is

and the linear response is given as follows:
2.3. Nonlinear Growth Rate of the Nonlocal Decay AW = KAW1 + KSW2
Here we study the nonlinear decay of MHD AWs into KAWs and KSWs. In what follows, the pump AW's parameters are without indices, KAW's parameters are with index "1," and KSW's parameters are with index "2." It is convenient to use the normalized magnetic B1⊥/B0 and density n2/n0 amplitudes as independent variables for KAWs and KSWs, respectively. The pump MHD AW is described by B⊥/B0 and propagates in the direction of B0. Within approximations made in our study, the decay properties of the pump MHD AW propagating in the opposite direction are the same.
Then, using Equations (20)–(25) with scalar nonlinearities proportional to ![$\left[ \mathbf {B}_{\perp }\times \mathbf {k} _{1\perp }\right] \cdot \mathbf {\hat{z}}$](https://content.cld.iop.org/journals/0004-637X/785/2/139/revision1/apj486709ieqn9.gif) , the nonlinear dispersion equations are obtained for KAWs,
, the nonlinear dispersion equations are obtained for KAWs,
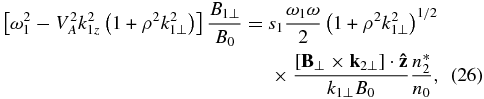
and for KSW,
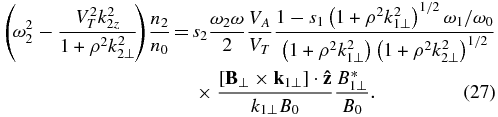
Noting that k2⊥ ≈ −k1⊥for the nonlocal interaction and combining the above equations, we obtain the growth rate of nonlinearly driven KAWs and KSWs:
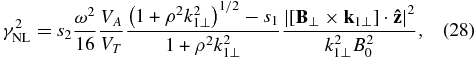
where s1 and s2 are the propagation directions of the product waves KAW1 and KSW2 with respect to the propagation direction of the pump wave AW (sα = −1 for the αth wave propagating against the pump and vice versa).
From dispersion relations (Equations (21) and (24)), one can see that the resonant conditions k = k1 + k2 and ω = ω1 + ω2 can be satisfied with forward KSW (s2 = 1), but not with backward KSW (s2 = −1). On the contrary, two decay channels involving forward (s1 = 1) and backward (s1 = −1) KAWs are allowed. Therefore, there are two possible decay channels for the MHD AW pump: (1) into forward KAW and KSW (s1 = s2 = 1), and (2) into backward KAW (s1 = −1) and forward KSW (s2 = 1). The corresponding parallelograms reflecting resonant conditions in the (ω, kz) plane are presented in Figure 1.
Figure 1. Two possible decay channels for the pump MHD AW: (1) into co-propagating KAW (s1 = 1) and KSW (s2 = 1), and (2) into counter-propagating KAW (s1 = −1) and co-propagating KSW (s2 = 1).
Download figure:
Standard image High-resolution image3. PRELIMINARY ANALYSIS: DECAY INTO NON-DISSIPATIVE WAVES
The growth rate dependence on the perpendicular wavenumbers of the product kinetic waves is axially asymmetric because of the factor
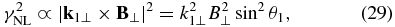
where θ1 is the angle between k1⊥ and B⊥. Therefore, the wave vectors of KAWs and KSWs generated by the scalar nonlinearities are elongated along the normal to the pump magnetic field, k1, 2⊥⊥B⊥.
Substituting Equation (29) in Equation (28), we obtain the normalized nonlinear pumping rate
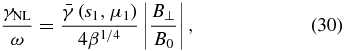
where μ1 = ρk1⊥ ≃ ρk2⊥ is the normalized perpendicular wavenumber of the kinetic-scale waves, and
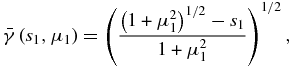
is the profile function showing the wavenumber dependence of γNL. The growth rate (Equation (30)) is already maximized with respect to the azimuthal angle θ1 (the θ1-dependence attains a maximum at θ1 ≃ π/2).
The profile function  has a maximum
has a maximum  at μ1 = μm- = 0 for counter-propagating KAWs, which is actually a MHD limit where our results are consistent with the results by Galeev & Oraevskii (1963). For co-propagating AWs, the maximum
at μ1 = μm- = 0 for counter-propagating KAWs, which is actually a MHD limit where our results are consistent with the results by Galeev & Oraevskii (1963). For co-propagating AWs, the maximum 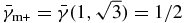 is attained at
is attained at 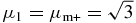 . The pumping rate tends to zero in the limit μ1 → ∞, where
. The pumping rate tends to zero in the limit μ1 → ∞, where 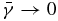 for both co- and counter-propagating product KAWs, s1 = ±1.
for both co- and counter-propagating product KAWs, s1 = ±1.
The normalized pumping rate γNL/ω as function of μi1 = ρik1⊥ (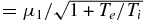 ) is shown in Figure 2 for particular plasma and pump wave parameters. As is seen from Figure 2, at small μi1 the nonlinear pumping rate for co-propagating KAWs first increases with increasing μi1, attains a maximum γNL/ω ≃ 0.075 at μi1 ≃ 1.2, and then gradually decays as μi1 grows further. The pumping rate into counter-propagating KAW monotonously decreases starting from the maximum γNL/ω ≃ 0.22 at μi1 = 0. The scaling at large μi1 ≫ 1 is the same in both cases,
) is shown in Figure 2 for particular plasma and pump wave parameters. As is seen from Figure 2, at small μi1 the nonlinear pumping rate for co-propagating KAWs first increases with increasing μi1, attains a maximum γNL/ω ≃ 0.075 at μi1 ≃ 1.2, and then gradually decays as μi1 grows further. The pumping rate into counter-propagating KAW monotonously decreases starting from the maximum γNL/ω ≃ 0.22 at μi1 = 0. The scaling at large μi1 ≫ 1 is the same in both cases,  , and γNL(s1 = −1) > γNL(s1 = 1) everywhere. Te/Ti = 1 was assumed for the above estimations, and the behavior is similar to other values of Te/Ti. The maximal pumping rate is decreased and shifted to lower μi1 at the larger temperature ratio Te/Ti = 3. For all values of Te/Ti, the nonlinear pumping of energy into counter-propagating KAWs is somehow stronger than that into the co-propagating KAWs.
, and γNL(s1 = −1) > γNL(s1 = 1) everywhere. Te/Ti = 1 was assumed for the above estimations, and the behavior is similar to other values of Te/Ti. The maximal pumping rate is decreased and shifted to lower μi1 at the larger temperature ratio Te/Ti = 3. For all values of Te/Ti, the nonlinear pumping of energy into counter-propagating KAWs is somehow stronger than that into the co-propagating KAWs.
Figure 2. Relative nonlinear pumping rate of energy into KAWs and KSWs, 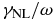 , as function of the normalized wavenumber
, as function of the normalized wavenumber  . The nonlinear pumping rate into co-propagating KAWs (s1 = 1) is shown by solid line, and into counter-propagating KAWs (s1 = −1) is shown by the dashed line. The temperature ratio Te/Ti = 1 and 3; the ion plasma beta
. The nonlinear pumping rate into co-propagating KAWs (s1 = 1) is shown by solid line, and into counter-propagating KAWs (s1 = −1) is shown by the dashed line. The temperature ratio Te/Ti = 1 and 3; the ion plasma beta 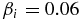 . The nonlinear pumping into counter-propagating KAWs is two to three times stronger.
. The nonlinear pumping into counter-propagating KAWs is two to three times stronger.
Download figure:
Standard image High-resolution imageSummarizing the above results, in the case of weak or no dissipation, the pump AW will mainly generate resonant KAWs and KSWs in the vicinity of the above maxima. The resulting pumping rates per one wave period are
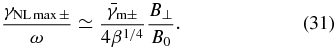
These fastest growing KAWs and KSWs determine the effective decay rate for the pump AW. At larger μi1 > μm ±, the pumping rate γNLmax ± gradually decreases. Obviously, the nonlinear pumping rates are not very affected by β that comes with the power index 1/4, such that the coefficient β1/4 ∼ 1 in the wide range 0.1 < β < 1, in which case
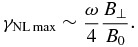
Therefore, the most significant explicit influence of the pump wave parameters comes from the linear γNLmax dependence of the pump magnetic amplitude B⊥. With the pump wave amplitude B⊥/B0 = 0.4, we obtain a high growth rate γNLmax ∼ 0.1ω. Although the above relation indicates that the nonlinear decay of the MHD AW can occur even for very small B⊥, the actual dissipation of kinetic waves imposes a decay condition B⊥ > Bthr with a finite threshold amplitude Bthr, as is shown below. There are also implicit restrictions imposed by the small wave frequencies, which will be discussed below.
The total decay rate accounting for the damping of product waves γL1 and γL2 is
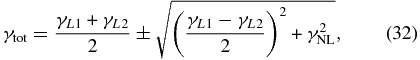
where γNL is given by Equation (30). To study nonlinear decay in weakly collisional plasmas, such as solar wind and magnetosphere, we must obtain expressions for damping rates of KAWs (γL1) and KSWs (γL2) in the kinetic plasma model. The analysis of the decay accounting for dissipative processes is given in the following sections.
4. COLLISIONLESS DISSIPATION OF KAWs AND KSWs
In the low-frequency domain, 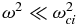 , the dissipation is dominated by the Landau damping. The corresponding damping rates for KAWs and KSWs can be presented as γLα = ωαgα, where α = 1 for KAW, α = 2 for KSW, and gα = gα(μi) depend only on the perpendicular wavenumber μi = ρik⊥ but do not depend on other wave parameters. In Maxwellian plasmas, KAWs dissipate with the rate (see, e.g., Voitenko & Goossens 2006)
, the dissipation is dominated by the Landau damping. The corresponding damping rates for KAWs and KSWs can be presented as γLα = ωαgα, where α = 1 for KAW, α = 2 for KSW, and gα = gα(μi) depend only on the perpendicular wavenumber μi = ρik⊥ but do not depend on other wave parameters. In Maxwellian plasmas, KAWs dissipate with the rate (see, e.g., Voitenko & Goossens 2006)
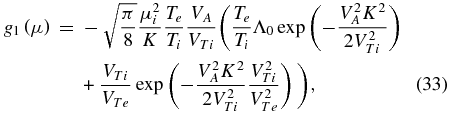
where 
 is the zero-order Bessel function,
is the zero-order Bessel function, 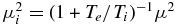 , and the KAW dispersion function
, and the KAW dispersion function 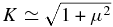 . The first term in g1(μi) is due to ion Landau damping and the second term is due to electron Landau damping (effects of finite electron gyroradius are neglected).
. The first term in g1(μi) is due to ion Landau damping and the second term is due to electron Landau damping (effects of finite electron gyroradius are neglected).
For KSWs, we will use the low-frequency kinetic dispersion equation
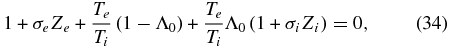
obtained from the electrostatic approximation (right-hand side of Equation (5) by Voitenko & Goossens 2003). In Equation (34), 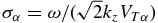 , and Zα = Z(σα) is the plasma dispersion function of the αth species. In order to find useful analytical expressions for KSW, it is customary to assume a non-isothermal plasma with Te/Ti ≫ 1 and expand Ze (Zi) in small σe (large σi) series, keeping first terms.
, and Zα = Z(σα) is the plasma dispersion function of the αth species. In order to find useful analytical expressions for KSW, it is customary to assume a non-isothermal plasma with Te/Ti ≫ 1 and expand Ze (Zi) in small σe (large σi) series, keeping first terms.
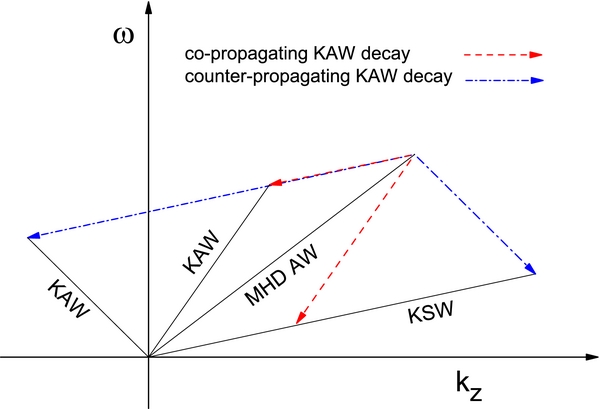
Unfortunately, there is no simple analytical solution g2(μi) for KSWs in isothermal plasmas with Te ∼ Ti, which is the most interesting case. This is because the KSW phase velocity in this case is close to the ion thermal speed (σi ∼ 1), and hence the plasma dispersion function Z(σi) cannot be expanded in the large argument series. We therefore solved Equation (34) numerically and found the following fit to the numerical solution:
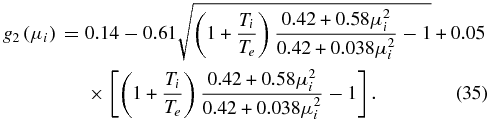
Figure 3 presents the exact numerical solution of Equation (34) and its parametric fit (Equation (35)) for three values of the temperature ratio Te/Ti = 1/3, 1, and 3. In the wide range of μi2 = ρik2⊥ from 0 to about 4, the fit and the numerical solution remain close to each other for the cases Te/Ti = 1 and 3; they are closer with larger Te/Ti. For the low-temperature ratio Te/Ti = 1/3, the fit declines and the damping rate is underestimated at μi2 > 2.5. In general, with increasing  , the KAW1 Landau damping |γL1| increases. Also, the KSW2 phase velocity Vph2 decreases toward the thermal proton velocity making |γL2| larger.
, the KAW1 Landau damping |γL1| increases. Also, the KSW2 phase velocity Vph2 decreases toward the thermal proton velocity making |γL2| larger.
Figure 3. Numerical solution (dashed lines) of the kinetic dispersion equation for KSWs (Equation (34)) and the parametric fit (Equation (35)) (solid line) for the temperature ratios Te/Ti = 1/3, 1, and 3.
Download figure:
Standard image High-resolution image5. NONLINEAR GENERATION OF DISSIPATIVE KINETIC WAVES BY THE PARAMETRIC DECAY OF MHD AWs
For the co-propagating KAW decay, the collisionless damping of KAWs and KSWs suppresses the wave growth at large 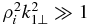 and small
and small 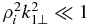 , where the nonlinear pumping drops faster than the linear damping. As a result, the nonlinear pumping can overcome the linear damping only in a limited region of perpendicular wavenumbers around
, where the nonlinear pumping drops faster than the linear damping. As a result, the nonlinear pumping can overcome the linear damping only in a limited region of perpendicular wavenumbers around  . For the counter-propagating KAW decay, the collisionless damping exceeds the wave growth only at large
. For the counter-propagating KAW decay, the collisionless damping exceeds the wave growth only at large 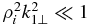 . To find the perpendicular wavenumbers favorable for the wave growth, and the corresponding total growth rate, we rewrite Equation (32) in terms of g1, g2, and γNL:
. To find the perpendicular wavenumbers favorable for the wave growth, and the corresponding total growth rate, we rewrite Equation (32) in terms of g1, g2, and γNL:
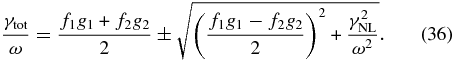
In low-β plasmas, conditions of the spatio-temporal resonance fix frequencies of nonlinearly driven waves at

where s1 is the sign of k1z: s1 = 1 for k1z > 0 (co-propagating product KAW), s1 = −1 for k1z < 0 (counter-propagating KAW).
Expression (36) provides a basis for our further analysis of the total growth rate for the nonlocal decay AW = KAW + KSW, including collisionless dissipative effects. In what follows we will focus on the co-propagating KAW decay found in the present study.
In Figure 4, we first show the perpendicular wavenumber dependence γtot = γtot(s1 = 1, ρik1⊥) in comparison to the nonlinear pumping rate γNL. The linear damping rates for KAWs (γL1) and for KSWs (γL2) are also shown for comparison. Note that all these rates are normalized by the pump wave frequency ω. It appears that the linear damping not only reduces the growth rate, but also shifts its maximum toward lower perpendicular wavenumbers ρik1⊥ ≃ ρik2⊥ of the nonlinearly driven waves. The KSW damping is stronger near the maximum of the decay rate, but γL1 becomes dominant at larger μi1, where γL2 saturates (not shown). Another consequence of the wave dissipation is a significantly smaller wavenumber spectrum of the instability, γtot, compared to the wide spectrum of pumping γNL. In accordance with Equation (31), the MHD wave should generate kinetic-scale KAWs and KSWs at the rate γNLmax ≈ 0.04ω.
Figure 4. Total growth rate of the co-propagating KAWs, 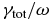 , as function of normalized perpendicular wavenumber
, as function of normalized perpendicular wavenumber 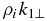 in the isothermal low-
in the isothermal low- plasma with
plasma with 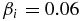 and Te = Ti. The magnetic amplitude of the pump MHD AW is B⊥/B0 = 0.3. The nonlinear pumping rate
and Te = Ti. The magnetic amplitude of the pump MHD AW is B⊥/B0 = 0.3. The nonlinear pumping rate 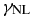 and Landau damping rates
and Landau damping rates  and
and 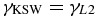 of the nonlinearly generated KAWs and KSWs are also shown for reference.
of the nonlinearly generated KAWs and KSWs are also shown for reference.
Download figure:
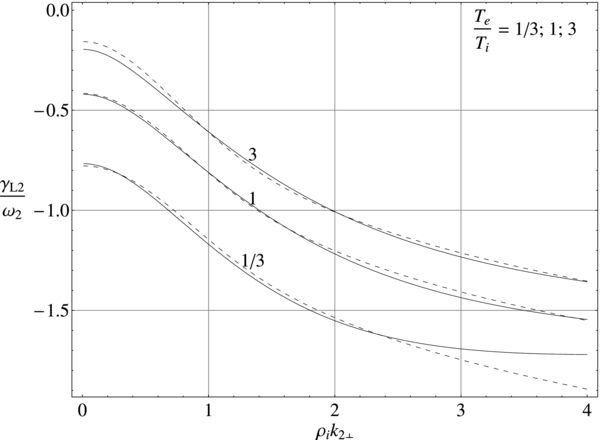
Standard image High-resolution imageNext, we compare the growth rates of co-propagating KAWs for three different values of Te/Ti (see Figure 5). The growth rate is larger for lower Te/Ti, which results from the competition between stronger pumping and stronger damping at lower Te/Ti. Again, the wavenumber spectra of the decay is significantly smaller because the damping suppresses the driving everywhere except for maximum.
Figure 5. Total growth rate 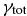 of the co-propagating (s1 = 1) product KAWs and KSWs as function of the normalized perpendicular wavenumber
of the co-propagating (s1 = 1) product KAWs and KSWs as function of the normalized perpendicular wavenumber 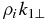 . The plasma is low-
. The plasma is low-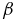 with
with 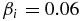 and isotropic, but Te/Ti assumes three different values Te/Ti = 1/3, 1, and 3. The MHD wave amplitude B⊥/B = 0.3.
and isotropic, but Te/Ti assumes three different values Te/Ti = 1/3, 1, and 3. The MHD wave amplitude B⊥/B = 0.3.
Download figure:
Standard image High-resolution imageFinally, we analyze behavior of the maximum growth rate γmax = γmax (B⊥/B0, ω, βi, Te/Ti), which is given by
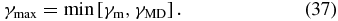
Here

is the maximum attained by the growth rate γtot(μ) of the ordinary parametric decay, and
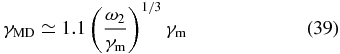
is the maximum growth rate of the modified parametric decay. In expressions (37)–(39), a modified decay formalism is taken into account. As explained by Oraevsky (1983), the modified decay formalism and the corresponding growth rate (Equation (39)) should be applied once the ordinary decay rate overcomes the lowest frequency participating in the decay. Since the lowest frequency in our case is the frequency of the product KSW, at γm > ω2 the actual growth rate becomes Equation (39).
It is convenient to normalize all γ's by the MHD AW frequency ω. The relative growth rate γmax /ω is shown in Figure 6 as function of the ion plasma beta 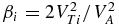 . It is seen that the process enhances toward lower βi and weakens toward higher βi, but the overall difference is not very large.
. It is seen that the process enhances toward lower βi and weakens toward higher βi, but the overall difference is not very large.
Figure 6. Maximum relative growth rates  of the co-propagating KAWs as functions of
of the co-propagating KAWs as functions of 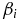 at two MHD AW amplitudes B⊥/B0 = 0.2 and 0.5. The temperature ratio Te/Ti = 1. In the bifurcation points, the decay switches to the regime of modified decay. The ordinary decay is shown for comparison by the dashed lines.
at two MHD AW amplitudes B⊥/B0 = 0.2 and 0.5. The temperature ratio Te/Ti = 1. In the bifurcation points, the decay switches to the regime of modified decay. The ordinary decay is shown for comparison by the dashed lines.
Download figure:
Standard image High-resolution imageAs shown in Figure 6, there is a transition to the modified decay at low βi where the dependence becomes more complex. The transition occurs when the ordinary growth rate becomes equal to the KSW frequency. The modified parametric decay operates in the pump frequency range below the transition frequency and causes the decay rate to decrease (the ordinary growth rate in this frequency range would be faster, as shown for comparison by the dashed lines). The ordinary decay operates at larger βi.
Formally, one can find the decay threshold by setting γmax = 0 and solving for Bthr/B0. However, given the limited time of the MHD AW existence, as well as various decorrelation mechanisms, we decided to use a more realistic conventional threshold calculated at γmax = 0.01ω. This choice means that the process should be faster than 100 periods of the pump MHD AW. We consider how this threshold behaves by solving γmax = 0.01ω for Bthr/B0 and varying the ion plasma beta βi. The result is shown in Figure 7. The electron/ion temperature ratio Te/Ti reduces the threshold (hence enforce the decay) at Te/Ti > 1, which is explained by the weakening of Landau damping.
Figure 7. Conventional threshold of the co-propagating decay Bthr/B0 calculated from the condition 
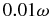 , as function of the ion plasma beta
, as function of the ion plasma beta 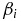 . The threshold at lower Te/Ti = 1 (solid lines) is lower than at Te/Ti = 3.
. The threshold at lower Te/Ti = 1 (solid lines) is lower than at Te/Ti = 3.
Download figure:
Standard image High-resolution image6. DISCUSSION
It is instructive to compare our nonlocal MHD-kinetic decay (Equation (31)) into backward KAW and forward KSW with the local MHD decay (Equation (1)) involving backward AW and forward SW (Galeev & Oraevskii 1963). By taking the MHD limit ρik1⊥ → 0 in the kinetic growth rate (Equation (31)), we recover the MHD result (Equation (1)) by Galeev & Oraevskii (1963). The maximum is attained at ρik1⊥ = 0, but the peak is not sharp and the growth rate of kinetic-scale waves at ρik1⊥ = 1 is only by factor 0.7 smaller than at maximum.
On the contrary, the co-propagating decay develops fastest at ρik1⊥ ∼ 1, whereas its MHD counterpart does not exist. The co-propagating decay of MHD AWs is therefore intrinsically nonlocal and only generates kinetic waves. Although the (kinetic) co-propagating growth rate is formally almost three times smaller than the counter-propagating MHD one, the actual generation of kinetic waves is not necessarily weaker. For example, AWs in the solar wind usually have finite correlation lengths lz ∼ λz ∼ 2π/kz, which limits their linear correlation time and hence the time available for the waves to interact nonlinearly. In particular, the correlation time for counter-propagating AWs is at least two times shorter than for co-propagating AWs, which favors the co-propagating decay and can make it dominant. These effects related to linear decorrelation need further investigation (e.g., using the random phase approach).
The nonlinear generation of KAWs and KSWs by the Alfvénic pump wave has been previously studied by Hasegawa & Chen (1976). However, the pump AW considered by Hasegawa & Chen (1976) was already in the kinetic regime, i.e., it was a KAW. It is clear that the growth rate found by Hasegawa & Chen (1976) vanishes in the limit k⊥⇀0, which means that only a local nonlinear interaction was captured. The same approximation has been used by many other authors (see, e.g., Brodin et al. 2006; Kryshtal' et al. 2007; Kumar & Sharma 2011), which did not allow them to capture the nonlocal interaction. We kept the nonlinear terms neglected by previous authors, which dominate at large k⊥ of product waves and lead to the essentially nonlocal interactions.
Decay of parallel-propagating AWs into oblique Alfvén and density waves was recently observed in the two-dimensional hybrid simulations by Gao et al. (2013). We believe that Gao et al. have captured another decay, which is much slower than the nonlocal decay we study here. Indeed, with parameters used by Gao et al. in their run 1, our nonlocal decay would generate oblique product waves within the time scale tωci < 1000, well before the oblique waves appear in Figure 2 by Gao et al. (2013). Also, the perpendicular wavenumbers generated by our decay, ρik1⊥ ∼ 1, are much larger than those observed in the simulations, ρik1⊥ ∼ 0.01. Waves with such large wavenumbers as ours (ρik1⊥ ∼ 1) could not be captured by these hybrid simulations because of their insufficient spatial resolution, limited by the ion inertial length.
In the present study, we are focused on the initial stage of the three-wave parametric decay where the parallel transport appears to be inefficient. Since this process cannot contribute to the small-scale parallel component observed by He et al. (2011) and Podesta & Gary (2011), other mechanism(s) should be involved. Recent simulations by Gao et al. (2014) suggest that this parallel component can be generated at the later stages when the modulation instability develops due to four-wave interactions.
The close analog of the process we study here is the nonlocal decay AW = KAW + KAW studied by Voitenko & Goossens (2005) at very low β < me/mi. Similar to our decay, the decay considered by Voitenko & Goossens (2005) is efficient for parallel-propagating MHD AWs (k⊥ = 0) and is essentially nonlocal, generating highly oblique kinetic waves. There is, however, a principal difference: Voitenko & Goossens considered nonlinearities proportional to k1⊥· B⊥, whereas we kept the terms ∝k1⊥× B⊥. As a consequence, our decay generates k1⊥⊥B⊥, which is opposite to the case k1⊥∥B⊥ by Voitenko & Goossens. Magnetic polarization is also different: B1⊥∥B⊥ in our case, and B1⊥⊥B⊥ in the case by Voitenko & Goossens. In the near future, we plan to extend our investigation to include the nonlinearities ∝k1⊥· B⊥.
Regardless of which decay dominates, the MHD AW spectrum with a preferred polarization direction should generate a spectrum of KAWs that are also polarized. The MHD AW anisotropy is indeed observed in the solar wind (Belcher & Davis 1971), and can either be a consequence of the sampling effect, or an inherent property of the MHD turbulence (Turner et al. 2012). However, we do not know of any correlation studies comparing simultaneously measured wave polarizations at MHD and kinetic scales, which would allow us to check if one of the above trends exists.
The fraction of the MHD wave energy that will be deposited into KAWs and KSWs via nonlocal coupling depends on the correlation times of MHD AWs. If the MHD pump waves keep their identity for a sufficiently long time, comparable to the nonlinear growth time of the kinetic waves, the nonlocal decay can be fulfilled in one single step and the related spectral transport is very efficient. This situation can be compared with the strong turbulence cascade but even more efficient because, in a single step, it transports energy over a much wider interval of scales. In the opposite situation, when the pump wave decorrelates faster than the kinetic waves grow, the nonlocal transport proceeds in many uncorrelated steps as in the weak turbulence. The more intermittent are local interactions among MHD AWs, the longer they exist, and hence the stronger is the direct nonlinear coupling of the MHD wave energy into kinetic scales.
Recent observations of the solar wind have revealed "standalone" AWs co-existent with the regular background MHD turbulence (Ghosh et al. 2009). These "standalone" AWs keep their coherency longer than the regular turbulent fluctuation because their spatio-temporal and amplitude proportions do not fit those of regular turbulent fluctuations and hence their nonlinear interaction with the background turbulence is inefficient. Simultaneous observations of such elevated AWs and KAWs at the proton gyroscale could help distinguishing the nonlocal transport we discuss here.
7. CONCLUSIONS
In the framework of parametric decay formalism, we investigated a nonlinear generation of small-scale KAWs and KSWs by large-scale MHD AWs. A new decay channel for MHD AW is found into forward kinetic-scale KAW and KSW. The previously known decay of MHD AW into backward MHD AW and forward MHD SW is extended to include the oblique kinetic regime. KAWs propagating against the pump MHD AW are generated at about the same rate as co-propagating KAWs and can contribute to the increasing fraction of the sunward waves as k1⊥ approaches the ion gyroscale in the solar wind. The MHD decay by Galeev & Oraevskii (1963) is recovered by our counter-propagating kinetic decay in the MHD limit ρik1⊥ → 0. The collisionless dissipation (Landau damping) of the product KAWs and KSWs is strong and reduces their growth rate. Nevertheless, the MHD AWs with the parameters representative for the solar wind are efficient in generating small-scale KAWs and KSWs at ρik2⊥ ∼ ρik1⊥ ∼ 1. With reasonable MHD wave amplitudes B ∼ 0.3B0, the growth rate of co-propagating kinetic waves can be quite high, γ ∼ 0.1ω, and can provide an efficient mechanism for the nonlocal spectral transport from MHD to kinetic scales.
The main features of the nonlocal MHD/kinetic decay into co-propagating waves and related spectral transport are as follows.
- 1.The nonlocal transport occurs in the cross-field direction such that the perpendicular wavenumbers of excited kinetic waves are much larger than the original wavenumbers of MHD AWs: k2⊥ ≃ k1⊥ ≫ k⊥. There is no nonlocal transport of the AW power in the parallel direction, k1∥ ∼ k∥.
- 2.The kinetic-scale KAWs and KSWs are most efficiently excited at the wavenumber ρik2⊥ ≃ ρik1⊥ ≲ 1 defined by competition between the nonlinear pumping γNL and the counter-acting dissipation γL1, 2.
- 3.Perpendicular wave vectors of nonlinearly generated kinetic waves tend to be normal to the pump magnetic field, k1⊥⊥B⊥.
- 4.The process is not sensitive to the pump perpendicular wavenumber k⊥ and is efficient for the parallel-propagating MHD AWs, k⊥ = 0.
- 5.The high-frequency/high-amplitude MHD AWs are more efficient generators of kinetic waves than the low-frequency/low-amplitude ones. This property makes the process feasible for intermittent fluctuations arising in the solar wind turbulence at higher (but still MHD) frequencies.
- 6.The decay strengthens toward lower β, which could make it more efficient within 1 AU closer to the Sun where β is rapidly decreasing.
We believe that vectorial nonlinearities proportional to ![$\left[ \mathbf {k} _{1\perp }\times \mathbf {k}_{\perp }\right] \cdot \mathbf {\hat{z}}$](https://content.cld.iop.org/journals/0004-637X/785/2/139/revision1/apj486709ieqn48.gif) can contribute to the nonlocal interaction as well and we are going to study them in the near future. One should note that the scalar and vectorial decays occupy different domains in the wave vector space, which makes their separate investigations possible.
can contribute to the nonlocal interaction as well and we are going to study them in the near future. One should note that the scalar and vectorial decays occupy different domains in the wave vector space, which makes their separate investigations possible.
This research was supported by the Belgian Federal Science Policy Office via IAP Programme (project P7/08 CHARM), by the European Commission via FP7 Program (project 313038 STORM), by the NSFC under grant No. 11303099, No.11373070, and No. 41074107, by the MSTC under grant No. 2011CB811402, by the NSF of Jiangsu Province under grant No. BK2012495, and by the Key Laboratory of Solar Activity at NAO, CAS, under grant No. KLSA201304.