Effects of Elasticity on Cell Proliferation in a Tissue-Engineering Scaffold Pore

Abstract

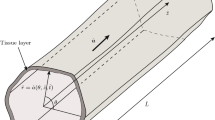
Scaffolds engineered for in vitro tissue engineering consist of multiple pores where cells can migrate along with nutrient-rich culture medium. The presence of the nutrient medium throughout the scaffold pores promotes cell proliferation, and this process depends on several factors such as scaffold geometry, nutrient medium flow rate, shear stress, cell-scaffold focal adhesions and elastic properties of the scaffold material. While numerous studies have addressed the first four factors, the mathematical approach described herein focuses on cell proliferation rate in elastic scaffolds, under constant flux of nutrients. As cells proliferate, the scaffold pores radius shrinks and thus, in order to sustain the nutrient flux, the inlet applied pressure on the upstream side of the scaffold pore must be increased. This results in expansion of the elastic scaffold pore, which in turn further increases the rate of cell proliferation. Considering the elasticity of the scaffold, the pore deformation allows further cellular growth beyond that of inelastic conditions. In this paper, our objectives are as follows: (i) Develop a mathematical model for describing fluid dynamics, scaffold elasticity and cell proliferation for scaffolds consist of identical nearly cylindrical pores; (ii) Solve the models and then simulate cellular proliferation within an elastic pore. The simulation can emulate real life tissue growth in a scaffold and offer a solution which reduces the numerical burdens. Lastly, our results demonstrated are in qualitative agreement with experimental observations reported in the literature.

Appendices

Appendix A

In this appendix, we justify the assumption of the elasto-static condition described in Sect. 2.2. With the assumptions mentioned in Sect. 2.2, elastic pore deformation is described by the Navier–Cauchy equations as

$$\begin{aligned} \frac{E}{2(1+\nu )}\nabla ^2\varvec{\Omega } + \frac{E}{2(1+\nu )(1-2\nu )}\varvec{\nabla }(\varvec{\nabla }\cdot \varvec{\Omega })= \rho _m \frac{\partial ^2\varvec{\Omega }}{\partial t^2}, \end{aligned}$$

(A1)

where the displacement vector and the density of the elastic pore are represented by $\varvec{\Omega }=(\Omega _r,\Omega _\theta ,\Omega _z)$ and $\rho _m$, respectively. Young’s Modulus E, and Poisson’s ratio $\nu$ are used to quantify the compliance of the elastic construct. After applying the scalings given in (14), (24), (30) and dropping $\hat{}$, (A1) simplifies to

$$\begin{aligned} \nabla ^2\varvec{\Omega } + \frac{1}{(1-2\nu )}\varvec{\nabla }(\varvec{\nabla }\cdot \varvec{\Omega })= {\frac{2(1+\nu )\rho _m \lambda ^2}{E R^2}} \frac{\partial ^2\varvec{\Omega }}{\partial t^2}, \end{aligned}$$

(A2)

where $\varvec{\Omega }=(\Omega _r,\epsilon \Omega _\theta ,\Omega _z)$ is now the dimensionless displacement vector. The coefficient ${\frac{2(1+\nu )\rho _m \lambda ^2}{E R^2}\ll 1}$ according to the parameters’ values given in Table 1. Therefore, in the regime we are focusing on in this paper, the term $\frac{\partial ^2\varvec{\Omega }}{\partial t^2}$ can be set to zero, which is the elasto-static condition.

Appendix B

In this appendix, we present the detailed calculations of (45)-(48). We solve the solution for $a_0(z,t)$ and $\Lambda (z,t)$ by treating each (time) interval separately, and match the solutions in the different intervals by requiring that a(z, t) and $\Lambda (z,t)$ be continuous functions of t. The first part of (44), which is $\frac{\partial a_0(z,t)}{\partial t} = - \kappa _0 f+\frac{\partial \Omega _{r_0}(z,t)}{\partial t}$, can be solved as below. We begin by plugging f and $\Omega _{r_0}(z,t)$ from (32) and (43), respectively, into the first part of (44) to get

$$\begin{aligned} \frac{\partial a_0(z,t)}{\partial t} =\left\{ \begin{array}{lll} -\frac{F_1}{a_0(z,t)}+8\eta (1-z)\frac{\partial \left( {a_0^{-3}(z,t)}\right) }{\partial t},&{}\text{ if } &{} \frac{4}{{a_0^3(z,t)}}<\sigma _1,\\ -\frac{F_2}{a_0(z,t)}+8\eta (1-z)\frac{\partial \left( {a_0^{-3}(z,t)}\right) }{\partial t},&{}\text{ if } &{} \sigma _1\le \frac{4}{{a_0^3(z,t)}}<\sigma _2,\\ 8\eta (1-z)\frac{\partial \left( {a_0^{-3}(z,t)}\right) }{\partial t},&{}\text{ if } &{} \sigma _2\le \frac{4}{{a_0^3(z,t)}}. \end{array} \right. \end{aligned}$$

(B3)

Next, we multiply both sides of the first part of (B3) by $a_0$ and simplify the right hand side of the equation to obtain

$$\begin{aligned} a_0(z,t)\frac{\partial a_0(z,t)}{\partial t}=-F_1-24\eta (1-z)a_0^{-3}(z,t)\frac{\partial a_0(z,t)}{\partial t}. \end{aligned}$$

(B4)

Integrating both sides of (B4) with respect to t gives

$$\begin{aligned} \frac{1}{2}{a_0^2(z,t)}=-F_1t-24\eta (1-z)\frac{{a_0^{-2}(z,t)}}{-2}+c_1, \end{aligned}$$

(B5)

where $c_1$ can be determined by setting $t=0$ in (B5) as

$$\begin{aligned} c_1=\frac{1}{2}\left( a_{0}^2(z,0)-24\eta (1-z)a_0^{-2}(z,0)\right) . \end{aligned}$$

(B6)

Substituting $c_1$ into (B5) and multiplying both sides by $2a_0^2(z,t)$ gives a quadratic equation for $a_0^2(z,t)$:

$$\begin{aligned} a_0^4(z,t)+\left( 2F_1t-a_0^2(z,0)+24\eta (1-z)a_0^{-2}(z,0)\right) a_0^2(z,t)-24\eta (1-z)=0. \end{aligned}$$

(B7)

Solving (B7) for $a_0(z,t)$ in the time interval $0 \le t < t_{01}$ yields

$$\begin{aligned} \begin{aligned}&a_0(z,t)=\Bigg [-\left( F_1t-\frac{1}{2}a_0^2(z,0)+ 12\eta (1-z) a_0^{-2}(z,0)\right) \\&\quad +\left( \left( F_1t-\frac{1}{2}a_0^{2}(z,0) + 12\eta (1-z) a_0^{-2}(z,0)\right) ^2+24\eta (1-z)\right) ^{1/2}\Bigg ]^{1/2}. \end{aligned} \end{aligned}$$

(B8)

To find $t_{01}$, we set $\frac{4}{a_0^3(z,t_{01})}=\sigma _1$ and it is convenient to write it in the equivalent form

$$\begin{aligned} a_0^2(z,t_{01}) = \left( \frac{4}{\sigma _1}\right) ^{\frac{2}{3}}. \end{aligned}$$

(B9)

By evaluating (B8) for $t=t_{01}$ and using (B9), after some algebraic manipulations, we obtain

$$\begin{aligned} t_{01}= & {} \frac{1}{F_1}{\Bigg [} \frac{1}{2 \left( \frac{4}{\sigma _1}\right) ^{2/3}} \left( 24\eta (1-z)- \left( \frac{4}{\sigma _1}\right) ^{4/3}\right) + \frac{1}{2} a_0^2(z,0)\\{} & {} - 12\eta (1-z)a_0 ^{-2}(z,0) {\Bigg ]}. \end{aligned}$$

In order to solve the second part of (B3), we will follow a process similar to what we have done for the first part of (B3). Therefore, the second part of (B3) gives

$$\begin{aligned} \frac{1}{2}{a_0}(z,t)^2=-F_2t-24\eta (1-z)\frac{{a_0(z,t)}^{-2}}{-2}+c_2. \end{aligned}$$

(B10)

Similarly, we obtain $c_2$ by setting $t=t_{01}$. Substituting $c_2$ into (B10) and using $a_0(z,t_{01})=\left( \frac{4}{\sigma _1}\right) ^\frac{1}{3}$ together, the solution for $a_0(z,t)$ within the time interval $t_{01} \le t < t_{02}$ is

$$\begin{aligned} \begin{aligned}&a_0(z,t)=\Bigg [-\left( F_2(t-t_{0_1})+12\eta (1-z)\left( \frac{4}{\sigma _1}\right) ^{-2/3}-\frac{1}{2}\left( \frac{4}{\sigma _1}\right) ^{2/3}\right) \\&\quad +\left( \left( F_2(t-t_{0_1})+ 12\eta (1-z)\left( \frac{4}{\sigma _1}\right) ^{-2/3} -\frac{1}{2}\left( \frac{4}{\sigma _1}\right) ^{2/3}\right) ^2+24\eta (1-z)\right) ^{1/2} \Bigg ]^ {1/2}. \end{aligned} \end{aligned}$$

(B11)

Setting $t=t_{02}$ and using $\frac{4}{{a_0^3(z,t_{02})}}=\sigma _2$ in (B11), after some manipulations, we find

$$\begin{aligned}{} & {} t_{02}=t_{01}+\frac{1}{F_2}{\Bigg [}\frac{1}{2 \left( \frac{4}{\sigma _2}\right) ^{2/3}} \left( 24\eta (1-z)- \left( \frac{4}{\sigma _2}\right) ^{4/3}\right) +\frac{1}{2}\left( \frac{4}{\sigma _1}\right) ^{2/3}\\{} & {} \quad -12\eta (1-z)\left( \frac{4}{\sigma _1}\right) ^{-2/3}{\Bigg ].} \end{aligned}$$

Similar to the first and second parts of (B3), the third one gives

$$\begin{aligned} \frac{1}{2}{a_0(z,t)}^2=-24\eta (1-z)\frac{{a_0^{-2}(z,t)}}{-2}+c_3, \end{aligned}$$

(B12)

where $c_3$ should be determined. Since $a_0(z,t_{02})=(\frac{4}{\sigma _2})^{1/3}$, we find

$$\begin{aligned} c_3=\frac{1}{2}\left( \frac{4}{\sigma _2}\right) ^{2/3}-12\eta (1-z)\left( \frac{4}{\sigma _2}\right) ^{-2/3}, \end{aligned}$$

(B13)

and after some manipulations, we obtain

$$\begin{aligned} \begin{aligned}&a_0(z,t)=\Bigg [-\left( 12\eta (1-z) \left( \frac{4}{\sigma _2}\right) ^ {-2/3} - \frac{1}{2}\left( \frac{4}{\sigma _2}\right) ^{2/3}\right) \\&\quad +\left( \left( 12\eta (1-z) \left( \frac{4}{\sigma _2}\right) ^{-2/3}) - \frac{1}{2}\left( \frac{4}{\sigma _2}\right) ^{2/3}\right) ^2 +24\eta (1-z)\right) ^{1/2}\Bigg ]^{1/2},\quad t>t_{02} \end{aligned} \end{aligned}$$

(B14)

For the rest of this appendix, we show how to obtain (46). Using (32) and (39) in (44) yields

$$\begin{aligned} \frac{\partial \Lambda (z,t)}{\partial t}=\left\{ \begin{array}{lll} \frac{-n^2\Lambda (z,t) F_1}{a_0^2(z,0)-2F_1t},&{} \text{ if } &{} 0\le t<t_{01},\\ \frac{-n^2\Lambda (z,t) F_2}{a_0^2(z,0)-2(F_1-F_2)t_{01}-2F_2t}, &{}\text{ if } &{} t_{01} \le t<t_{02},\\ 0,&{} \text{ if } &{} t \ge t_{02}. \end{array} \right. \end{aligned}$$

(B15)

The first part of (B15) can be rewritten as

$$\begin{aligned} \frac{1}{{\Lambda (z,t)}}\frac{\partial \Lambda (z,t)}{\partial t}= \frac{-n^2 F_1}{a_0^2(z,0)-2F_1t}. \end{aligned}$$

(B16)

By integrating both sides of (B16) with respect to t, we obtain

$$\begin{aligned} \ln \vert \Lambda (z,t)\vert = \ln \vert a_0^2(z,0)-2F_1t \vert ^{n^2/2} + c_4, \end{aligned}$$

(B17)

where $c_4$ is an constant of integration and should be determined. After removing the absolute value bars in (B17), and by taking the exponential of both sides, we find that

$$\begin{aligned} \Lambda (z,t)=c_5\left( a_0^2(z,0)-2F_1t\right) ^{n^2/2}, \end{aligned}$$

(B18)

where $c_5 = e^{c_4}$. In order to satisfy the initial condition $\Lambda (z,0)$, we must choose $c_5 = \Lambda (z,0)/a_0^{n^2}(z,0)$. Using this value for $c_5$ in (B18), we obtain

$$\begin{aligned} \Lambda (z,t)=\Lambda (z,0) \big [1-2 F_1t/a_0^2(z,0) \big ]^{n^2/2}, \quad 0\le t<t_{01}. \end{aligned}$$

The next two parts of (B15) could be obtained in a similar fashion.