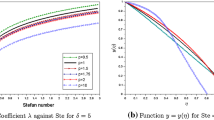
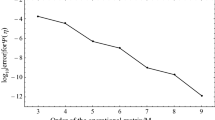
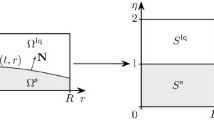
Abstract
Recently, in Tarzia (Thermal Sci 21A:1–11, 2017) for the classical two-phase Lamé–Clapeyron–Stefan problem an equivalence between the temperature and convective boundary conditions at the fixed face under a certain restriction was obtained. Motivated by this article we study the two-phase Stefan problem for a semi-infinite material with a latent heat defined as a power function of the position and a convective boundary condition at the fixed face. An exact solution is constructed using Kummer functions in case that an inequality for the convective transfer coefficient is satisfied generalizing recent works for the corresponding one-phase free boundary problem. We also consider the limit to our problem when that coefficient goes to infinity obtaining a new free boundary problem, which has been recently studied in Zhou et al. (J Eng Math 2017. https://doi.org/10.1007/s10665-017-9921-y).
Similar content being viewed by others
Abbreviations
- \(d_\mathrm{l}\), \(d_\mathrm{s}\) :
-
Diffusivity coefficient (m\(^2\)/s)
- \(h_0\) :
-
Coefficient that characterizes the heat transfer in condition (1.6) [kg/(\(^{\circ }\)Cs\(^{5/2}\))]
- \(k_\mathrm{l}\),\(k_\mathrm{s}\) :
-
Thermal conductivity [W/(m \(^{\circ }\)C)]
- s :
-
Position of the free front (m)
- t :
-
Time (s)
- \(T_{\infty }\) :
-
Coefficient that characterizes the bulk temperature in condition (1.6) [\(^{\circ }\)C/s\(^{\alpha /2}\)]
- \(T_i\) :
-
Coefficient that characterizes the initial temperature of the material in condition (1.7), [\(^{\circ }\)C/m\(^{\alpha }\)]
- x :
-
Spatial coordinate (m)
- \(\alpha \) :
-
Power of the position that characterizes the latent heat per unit volume (dimensionless)
- \(\gamma \) :
-
Coefficient that characterizes the latent heat per unit volume [kg/(s\(^2\)m\(^{\alpha +1}\))]
- \(\nu \) :
-
Coefficient that characterizes the free interface (dimensionless)
- \(\eta \) :
-
Similarity variable in expression (2.1) (dimensionless)
- \(\Psi _\mathrm{l},\Psi _\mathrm{s}\) :
-
Temperature (\(^{\circ }\)C).
- l :
-
Liquid phase
- s :
-
Solid phase
References
Abramowitz, M., Stegun, I.A. (eds.): Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. National Bureau of Standards, Washington (1964)
Alexiades, V., Solomon, A.D.: Mathematical Modelling of Melting and Freezing Processes. Hemisphere-Taylor Francis, Washington (1993)
Bollati, J., Tarzia, D.A.: Explicit solution for Stefan problem with latent heat depending on the position and a convective boundary condition at the fixed face using Kummer functions. Comm. Appl. Anal. (2017). https://arxiv.org/pdf/1610.09338v1.pdf
Briozzo, A.C., Natale, M.F.: Nonlinear Stefan problem with convective boundary condition in Storm’s materials. Z. Angrew. Math. Phys. 67(19), 1–11 (2016)
Cannon, J.R.: The One-Dimensional Heat Equation. Addison-Wesley, Menlo Park (1984)
Carslaw, H.S., Jaeger, C.J.: Conduction of Heat in Solids. Clarendon Press, Oxford (1959)
Crank, J.: Free and Moving Boundary Problem. Clarendon Press, Oxford (1984)
Gupta, S.C.: The Classical Stefan Problem. Basic Concepts, Modelling and Analysis. Elsevier, Amsterdam (2003)
Lorenzo-Trueba, J., Voller, V.R.: Analytical and numerical solution of a generalized Stefan Problem exhibiting two moving boundaries with application to ocean delta deformation. J. Math. Anal. Appl. 366, 538–549 (2010)
Lunardini, V.J.: Heat Transfer With Freezing and Thawing. Elsevier, London (1991)
Olver, F.W.J., Lozier, D.W., Boisvert, R.F., Clark, C.W.: NIST Handbook of Mathematical Functions. Cambridge University Press, New York (2010)
Perchuk, L.L.: Progress in Metamorphic and Magmatic Petrology. Cambridge University Press, Wallingford, UK (2003)
Primicerio, M.: Stefan-like problems with space-dependent latent heat. Meccanica 5, 187–190 (1970)
Rogers, C.: Application of a reciprocal transformation to a two-phase Stefan problem. J. Phys. A Math. Gen. 18, L105–L109 (1985)
Rubinstein, L.I.: The Stefan Problem. American Mathematical Society, Providence (1971)
Salva, N.N., Tarzia, D.A.: Explicit solution for a Stefan problem with variable latent heat and constant heat flux boundary conditions. J. Math. Anal. Appl. 379, 240–244 (2011)
Tao, L.N.: The exact solutions of some Stefan problems with prescribed heat flux. J. Appl. Mech. 48, 732–736 (1981)
Tarzia, D.A.: Relationship between Neumann solutions for two phase Lamé-Clapeyron-Stefan problems with convective and temperature boundary conditions. Thermal Sci. 21, 1–11 (2017)
Tarzia D.A.: Explicit and approximated solutions for heat and mass transfer problems with a moving interface. Chapter 20, in Advanced Topics in Mass Transfer, M. El-Amin (Ed.), InTech Open Access Publisher, Rijeka, pp 439–484 (2011)
Tarzia, D.A.: A bibliography on moving-free boundary problems for the heat-diffusion equation. The Stefan and related problems. MAT-Serie A 2, 1–297 (2000)
Tarzia, D.A.: An inequality for the coefficient \(\sigma \) of the free boundary \(s(t)=2\sigma \sqrt{t}\) of the Neumann solution for the two-phase Stefan problem. Quart. Appl. Math. 39, 491–497 (1982)
Voller, V.R., Swenson, J.B., Paola, C.: An analytical solution for a Stefan problem with variable latent heat. Int. J. Heat Mass Transf. 47, 5387–5390 (2004)
Zhou, Y., Shi, X., Zhou, G.: Exact solution for a two-phase problem with power-type latent heat. J. Eng. Math. (2017). https://doi.org/10.1007/s10665-017-9921-y
Zhou, Y., Wang, Y.J., Bu, W.K.: Exact solution for a Stefan problem with latent heat a power function of position. Int. J. Heat Mass Transf. 69, 451–454 (2014)
Zhou, Y., Xia, L.J.: Exact solution for Stefan problem with general power-type latent heat using Kummer function. Int. J. Heat Mass Transf. 84, 114–118 (2015)
Acknowledgements
The present work has been partially sponsored by the Projects PIP No. 0534 from CONICET-UA and ANPCyT PICTO Austral 2016 No. 0090, Rosario, Argentina.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bollati, J., Tarzia, D.A. Exact solution for a two-phase Stefan problem with variable latent heat and a convective boundary condition at the fixed face. Z. Angew. Math. Phys. 69, 38 (2018). https://doi.org/10.1007/s00033-018-0923-z
Received:
Published:
DOI: https://doi.org/10.1007/s00033-018-0923-z