Abstract
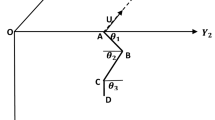
Faulting in a medium with an inhomogeneity is analysed applying two-dimensional models consisting of a shear crack in a presence of a circular inclusion. The stress drop and the stress intensity factor are calculated for mode II and III cracks of various positions in relation to the inclusion. The results demonstrate that the effect of an inhomogeneity on a shear zone strongly depends on the location of a zone for either mode II or mode III shear zone. This effect is mostly due to the spatial distribution of external effective shear stress around an inhomogeneity. Depending on the position, an inhomogeneity may have either a destabilizing effect (the stress intensity factor becomes greater) or a stabilizing influence (the stress intensity factor is decreased or faulting is prohibited so the inhomogeneity acts as an asperity or a barrier). There is a substantial difference, however, between mode II and mode III shear zones approaching an inhomogeneity centrally. Namely, the effect of inhomogeneity on the mode III shear zone located in the immediate vicinity of the inhomogeneity is in this case considerably more pronounced than that for mode II shear zone and depends to a far greater extent on the rigidity contrast between the inhomogeneity and the surrounding medium. Another important conclusion is that the quantitative effect of an inhomogeneity on faulting depends essentially on the initial value of the stress drop of a shear zone approaching an inhomogeneity, being decidedly higher for a shear zone of small stress drop. It means that in specified areas in the proximity of medium inhomogeneities one should expect substantially greater faulting activity in which weak events prevail than in other regions surrounding inhomogeneities where such activity should be distinctly reduced. Such conclusions apply to both high rigidity inhomogeneities, which, in particular, may be associated with intrusions from the upper mantle, and to low rigidity inhomogeneities such as volcanos. The present model sets forth the plausible explanation regarding why earthquakes from the same region are occasionally characterized by various values of the stress drop. The model also presents the quantitative insight concerning how heterogeneity of the medium, in the sense of spatial variation of elastic constants, affects faulting.
Similar content being viewed by others
References
Bilby, B. A., andEshelby, J. D.,Dislocations and the theory of fracture, InFracture: An Advance Treatise (ed. Liebowitz, H.) (Academic Press, New York 1968) pp. 99–182.
Boatwright, J. (1980),A Spectral Theory for Circular Seismic Source: Simple Estimates of the Source Dimension, Dynamic Stress Drop, and Radiated Seismic Energy, Bull. Seismol. Soc. Am.70, 1–27.
Brune, J. N. (1970),Tectonic Stress and Spectra of Seismic Shear Waves from Earthquakes, J. Geophys. Res.75, 4997–5009.
Brune, J. N. (1971),Correction, J. Geophys. Res.76, 5002.
Brune, J. N., Fletcher, J., Vernon, F., Haar, L., Hanks, T., andBerger, J.,Low stress drop earthquakes in the light of the new data from the Anza, California, telemetered digital array, InEarthquake Source Mechanics (eds. Das, S., Boatwright, J., and Scholz, C. H.) (Geophys. Mon. 37, Amer. Geophys. Un., Washington D.C. 1986) pp. 331–338.
Dundurs, J.,On the interaction of a screw dislocation with inhomogeneities, InRecent Advances in Engineering Sciences (ed. Eringen, E. C.) (Gordon and Breach, New York 1967) vol. 2, pp. 223–233.
Dundurs, J., andMura, T. (1964),Interaction Between an Edge Dislocation and a Circular Inclusion, J. Mech. Phys. Solids12, 177–189.
Erdögan, F., andGupta, G. D. (1972),On the Numerical Solution of Singular Integral Equations, Quart. J. Appl. Math.29, 525–534.
Fletcher, J. B., Haar, L. C., Vernon, F. L., Brune, J. N., Hanks, T. C., andBerger, J.,The effect of attenuation on the scaling of source parameters for earthquakes at Anza, California, InEarthquake Source Mechanics (eds. Das, S., Boatwright, J., and Scholz, C. H.) (Geophys. Mon. 37, Amer. Geophys. Un., Washington D.C. 1986), pp. 331–338.
Gough, D. I., andGough, W. I. (1987),Stress Near the Surface of the Earth, Ann. Rev. Earth Planet. Sci.15, 545–566.
Hanks, T. C., andMcGuire, R. K. (1981),The Character of High Frequency Strong Ground Motion, Bull. Seismol. Soc. Am.71, 2071–2096.
Healey, J. H., andPeake, L. G. (1975),Seismic Velocity Structure along a Section of the San Andreas Fault Near Bear Valley, California, Bull. Seismol. Soc. Am.65, 1177–1197.
Hirahara, K., Ikami, K., Ishida, A., andMikumo, T. (1989),Three-dimensional P-wave Velocity Structure Beneath Central Japan. Low-velocity Bodies in the Wedge Portion of the Upper Mantle above High Velocity Subducting Plates, Tectonophysics163, 63–73.
Kanamori, H., andAnderson, D. L. (1975),Theoretical Basis of Some Empirical Relations in Seismology, Bull. Seismol. Soc. Am.65, 1073–1096.
Mikumo, T., Wada, H., andKoizumi, M. (1988),Seismotectonics of the Hida Region, Central Honshu, Japan, Tectonophysics147, 95–119.
Mogi, K. (1962),Study of elastic Shocks Caused by the Fracture of Heterogeneous Materials and its Relation to Earthquake Phenomena, Bull. Earthq. Res. Tokyo Univ.40, 125–174.
Prohdel, C.,Structure of the earth's crust and upper mantle, InGeophysics of the Solid Earth, the Moon and the Planets (ed. Fuchs, K.) (Landold-Bornstein, Springer-Verlag, Berlin 1984) vol. v/2, subvol. a, pp. 97–205.
Rice, J. R.,Mathematical analysis in the mechanics of fracture, InFracture: An Advance Treatise (ed. Liebowitz, H.) (Academic Press, New York 1968) vol. 2, pp. 191–311.
Rudnicki, J. W. (1980),Fracture Mechanics Applied to Earth's Crust, Ann. Rev. Earth Planet. Sci.8, 489–525.
Rybicki, K. R. (1989),On Fault Slip Zones in the External Shear-field Separated by a High Rigidity Asperity (Barrier)—Inplane and Antiplane Strain Models, Geophys. J.96, 101–115.
Rybicki, K. R. (1990),On Faulting in the Presence of an Inhomogeneity-plane Strain Model, to be published in Acta Geophys. Pol.
Segall, P., andPollard, D. D. (1980),Mechanics of Discontinuous Faults, J. Geophys. Res.85, 4337–4350.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Rybicki, K.R. On faulting in a medium containing an inhomogeneity inplane and antiplane strain models. PAGEOPH 134, 283–301 (1990). https://doi.org/10.1007/BF00877002
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00877002