1 Introduction

The time-dependent mechanical behavior of polymeric materials is mainly expressed by the linear viscoelasticity theory when stresses/strains are small. The classical linear theory of viscoelasticity (Flügge 1967; Christensen 1982), which adequately describes the creep, relaxation, and loading-rate dependence of polymers, can be presented by two major forms: hereditary integrals or differential forms. This presentation, nevertheless, is limited to narrow loading rate and temperature regimes, while polymeric materials demonstrate a nonlinear response at relatively small strains. Due to the limited range where linearity is valid, nonlinear viscoelasticity theory is required to describe the polymeric materials response. A great number of equations relating stress and strain history have been developed. Among them, stress-strain relations in the form of multiple integral representation have received much attention (Green and Rivlin 1957; Green et al. 1959) and were hereafter utilized in several works (Ferry 1961; Ward and Onat 1963; Truesdell and Noll 1965). However, due to the complexity of this analysis in the case of strong nonlinearity, simple integral constitutive equations were developed, having similarities with the Boltzamnn superposition integrals introduced in linear viscoelasticity (Leaderman et al. 1963; Schapery 1966). This could be achieved since the time-dependent properties required could be estimated in the linear viscoelastic regime and introduced in the modified superposition theory by Leaderman et al. (1963) and later used also by Findley and Kholsla (1955). In addition, significant works related to more applicable models for nonlinear viscoelasticity have been developed (Findley and Onaran 1968; Mc Guirt and Lianis 1970). Within this context, progress has been made in developing mathematical models for the small strain regime under a specific narrow spectrum of strain rates (Lockett 1972). In the subsequent years, polymer’s nonlinear viscoelasticity has been the subject of a lot of works (Sane and Knauss 2001; Guedes 2011; Drozdov et al. 2009; Zacharatos and Kontou 2015; Zaoutsos and Papanicolaou 2010). In a work by Gacem et al. (2008), the nonlinear viscoelastic behavior of an elastomer in terms of creep tests at various stress levels was examined, whereas the long-term creep response on the basis of short-term creep tests was analyzed.

Within the context of constitutive modeling of inelasticity, Bahrololoumi et al. (2021b) adapted a large strain three-dimensional network alteration theory to understand and predict the inelastic behavior of elastomers during hydrolytic and thermo-oxidative aging. Bahrololoumi et al. (2022a, 2022b), making the assumption that the constitutive behavior of the material is offered by a modified network alteration constitutive model, developed a model that can predict the exact failure properties of cross-linked polymers in the course of aging at different times and temperatures. Accordingly, as presented by Bahrololoumi et al. (2022a, 2022b), kinetic equations describing damage of each aging mechanism are coupled into the network alteration modular concept to allow consideration of mechanical and environmental damage synergies on the constitutive response of the polymer matrix. As far as long-term viscoelastic response of polymeric materials is concerned, and particularly the improvement of the predictive capability of long-term stress relaxation of elastomers during thermo-oxidative ageing, a method to separate reversible and irreversible processes was adopted (Zaghdoudi et al. 2020; Dinari et al. 2021; Bahrololoumi et al. 2021a). The separation is performed through the analysis of compression set after tempering. On the basis of this separation, a numerical model for long-term stress relaxation during homogeneous ageing is proposed.

In another work (Starkova et al. 2012), creep and creep–recovery of epoxy/multi-wall carbon nanotube (MWCNTs) composites were investigated at various loadings, and the effect of MWCNTs on the creep response was examined. Moreover, Schapery’s analytical nonlinear model (Schapery 1966, 1969, 1997) was applied to describe the creep response of nanocomposites. The nonlinear viscoelasticity was extensively analyzed by Schapery, where four parameters that are stress and temperature dependent were employed to regulate the deviations from linear viscoelastic response. Zaoutsos et al. (1998) and Papanicolaou et al. (1999) presented a method for the estimation of Schapery’s model parameters.

Given the importance of nonlinear viscoelasticity, a significant issue is the reasons for the nonlinearity of materials. This can be attributed either to discontinuities or micro-cracking related to damage or to molecular forces affecting the macromolecular conformations, which do not occur as a result of internal damage. To this trend, Gacem et al. (2008) used a stress-dependent shift factor, introducing the effect of free volume and its effect on the material’s viscoelastic response. The concept of free volume lied in the fact that temperature, stress solvent concentration, etc. affect the fractional free volume in the material and consequently the mobility of inclusions and the change in fractional free volume if any one of internal variables is additive. Mobility of various inclusions generates macroscopic damping in material that can be included in time behavior laws. In this context, the creep resistance of polyamide 66 (PA66), reinforced with spherical nanoparticles, was studied in detail by Yang et al. (Part I, 2006a and Part II, 2006b) at various stress levels and temperatures.

The mechanisms of viscoelasticity of these nanocomposites were analyzed by means of thermal and stress activated process. In (Yang et al. Part II, 2006b), the modeling of creep deformation of PA66 and its nanocomposites were satisfactorily performed by employing Burgers model and Findley’s power law. The creep resistance exhibited by the nanocomposites was analyzed on the basis of the simulating parameters. Regarding the long-term creep response, Findley’s model and the time temperature superposition principle were capable of describing it adequately.

In the present research, particular aspects of polymer’s nonlinear viscoelasticity will be examined on the basis of a viscoelastic model presented and modified in previous works (Drozdov et al. 2009; Spathis and Kontou 2020, 2022). The study was performed with reference to selected experimental data taken from the literature. Applying proper modifications, it was found that the employed model is capable of simulating and predicting the nonlinear viscoelasticity in terms of short- and long-term creep strain data at various temperatures and stress levels. Additionally, the model was shown to describe different trends of the creep strain evolution with varying the imposed stress.

The first set of experimental data was the creep strain results at room temperature of epoxy resin reinforced with unidirectional carbon fibers at 90°, at five different stress levels (Zaoutsos and Papanicolaou 2010). These experiments were utilized to test the model’s validity in a wide time scale and various stresses. The second set of experimental results was those of polyamide 66 (PA66) and its nanocomposites (Yang et al., Part I, 2006a; Yang et al., Part II, 2006b), namely creep strain results at three different temperatures and three different stresses, as well as long-term creep data, by means of the creep master curve obtained by the time-temperature superposition principle. The nonlinear creep data were successfully simulated by the proposed model, while the compliance master curve could be captured with a good accuracy.

The third set of experimental data is taken from Gacem et al. (2008), and these results refer to the short-term nonlinear creep strain of an elastomer at various stresses. The long-term creep curve was also predicted within the frame of the present model.

In all cases, which refer to different polymeric structures and different experimental conditions, the model was shown to adequately describe/predict particular aspects of nonlinear creep behavior of the materials under investigation with a good accuracy and a low number of the required parameters, compared to widely known existing theories.

2 Constitutive analysis

One of the widely known constitutive theories for the nonlinear viscoelasticity was the Schapery’s theory (Schapery 1999), which for creep strain under uniaxial creep loading at a constant stress \(\sigma _{0}\) gives

$$ \varepsilon (t) = g_{0}D_{0}\sigma _{0} + g_{1}\int _{0}^{t} \Delta D(\xi - \xi ') \frac{dg_{2}(\sigma _{0})}{d\tau} d\tau , $$
(1)

where

$$ \xi = \int _{0}^{t} \frac{dt'}{\alpha _{\sigma}} \quad \mbox{and}\quad \xi ' = \int _{0}^{\tau} \frac{dt'}{\alpha _{\sigma}}, $$
(2)

where \(g_{0}\), \(g_{1}\), \(g_{2}\), \(\alpha _{\sigma}\) are nonlinear factors, which are stress and temperature dependent. \(D_{0}\) and \(D\) are the instantaneous compliance and the compliance function correspondingly, and \(\xi \) is the reduced time contributing to the nonlinear character of the constitutive equation (1).

A lot of works have analyzed and employed this theory for the description/prediction of nonlinear viscoelasticity of polymeric materials (e.g., Zaoutsos et al. 1998; Papanicolaou et al. 1999; Zaoutsos and Papanicolaou 2010).

Regarding constitutive modeling and referring to a polymeric network, a combined aging constitutive model was developed in (Bahrololoumi et al. 2021b) by supposing that damages induced by mechanical loads are composed of both permanent and reversible damages. Permanent damages are often induced by chemical changes in the network, such as detachment of cross-links and chain scission, while reversible damages are often induced by changes in matrix topology like chain slippage, detachment of physical bonds, or chain adsorption/detachment from particle surfaces.

In the present research, a viscoelastic model developed in previous works by Drozdov et al. (2009) and Spathis and Kontou (2018) is further analyzed. Within the framework of this model, it is assumed that the time-dependent response is the result of rearrangements between meso-regions, which consist of the polymeric structure. By this analysis, a three-dimensional time-dependent constitutive equation relating stress \(\sigma _{ij}(t)\) and strain \(\varepsilon _{ij}(t)\) was derived, and hereafter for a uniaxial loading it is expressed by

$$ \sigma (t) = \mu _{0} \left [ \varepsilon (t) - \int _{0}^{\infty} \Gamma (u) p(u) du \int _{0}^{t} \exp \left ( - \Gamma (u) (t - \tau ) \right ) \varepsilon (\tau ) d\tau \right ], $$
(3)

where \(\mu _{0}\) is the elastic stiffness. The entire analysis is based on the transient network model (Tanaka and Edwards 1992), whereas the kinematics relating the time evolution of the number of active domains has been introduced by Drozdov et al. (2009).

The quantity \(p(u)\) is the distribution function of energy levels of the meso-regions, and \(\Gamma (u)\) expresses the ratio of the number of meso-regions that rearrange per unit time to the total number of the meso-regions ensemble (Drozdov et al. 2003) and is given by

$$ \Gamma (u) = \gamma _{T} \exp [ - u]. $$
(4)

The term \(\exp [ - u]\) denotes the probability of a meso-region to cooperatively rearrange. It can be noticed that Eq. (3), despite being a linear one, has the form of a memory integral similar to Schapery’s equation (1). The quantity \(\gamma _{T}\) is the attempt rate that was considered to have an Arrhenius type equal to

$$ \gamma _{T} = \gamma _{0}\exp \left [ - \frac{\Delta H}{RT} \right ], $$
(5)

where \(\Delta H\) is the activation energy, \(R\) is the gas constant, \(T\) is the temperature. The pre-exponential factor \(\gamma _{0}\) is a constant. Arrhenius equation was utilized in a number of works (Bahrololoumi et al. 2021b, 2021a, 2022a, 2022b).

Following a trend analogous to previous theories by Eyring and his co-workers (Halsey et al. 1945), the nonlinear viscoelastic behavior of the materials will be treated by introducing the effect of stress on the basic parameters that affect the elastic and viscoelastic response of the material. In this context, we adopted the idea of Schapery and Eyring assuming a stress-dependent parameter \(\gamma _{T}(\sigma )\). Given that parameter \(\gamma _{T}\) determines the time evolution of the characteristic sizes, the main concept of this amendment is that the imposed stress \(\sigma \) modifies the potential barrier that the meso-domains will overcome to be transferred to a new state. Therefore \(\gamma _{T}(\sigma )\) is assumed to take the form

$$ \gamma _{T}(\sigma ) = \gamma _{0}\exp \left ( - \frac{\Delta H}{RT} \right ) \exp \left ( \pm \frac{\upsilon \sigma}{RT} \right ), $$
(6)

where \(\sigma \) is the imposed stress and \(\upsilon \) is the activation volume. Given that this expression determines the time evolution of characteristic sizes, the imposed stress \(\sigma \) modifies the potential barrier that the building blocks will overcome to be transferred to a new state.

The activation volume represents the volume of the polymer segments that have to cooperatively move for molecular rearrangements to occur.

It is widely known that the activation volume is a useful parameter that provides indication about the underlying molecular mechanisms. The activated rate process may be a common basis for analyzing the creep response (Yang et al. 2006a, 2006b).

Equation (6) can be rewritten as

$$ \gamma _{T}(\sigma ) = A\, \mathrm{Exp}(\pm \beta \sigma ) $$
(7)

or

$$ \ln \gamma _{\mathrm{T}}(\sigma ) = \ln A \pm \beta \sigma , $$
(8)

where \(A\) is a temperature-dependent constant with units in sec−1 and \(\beta \) is a constant in units (1/MPa). The ± denotes that the imposed stress can either facilitate or make it difficult for the transition to occur by reducing or increasing correspondingly the energy barrier height. According to the proposed model, a distribution of the energy barriers \(u\) is assumed. That is, the dynamic dams follow a specific distribution \(p(u)\) within the material, which, if known, determines accordingly the range of distribution of the recovery times. The specific distribution function to be used in the above description is selected to be a Gaussian distribution (Drozdov et al. 2009) with a mean value V and a standard deviation \(\Sigma \) as follows:

$$ p(u) = \mathrm{Exp}\,\left [ - \frac{1}{2}\left (\frac{u - V}{\Sigma} \right )^{2} \right ], $$
(9)

which is normalized by the expression

$$ {p}_{0} = \int _{0}^{\infty} {p}({u}) {du}. $$
(10)

The selection of the distribution function \(p(u)\) is a crucial point of the present analysis due to the fact that it includes both the distribution of the retardation/relaxation times and the particular effect of each one of them. An analogy to this can be found in the well-known Prony series method (Fernández et al. 2011), where a discrete spectrum of relaxation times \(\tau _{i}\) is taken into account accompanied by the specific weight factor of moduli \(E_{i}\) of the i number of Maxwell models. Regarding the physical meaning of the distribution parameters, it has been noticed that given that the distribution function is associated with the retardation times spectrum, the higher the standard deviation the longer retardation times are included in the creep process. Therefore, the proper selection of the standard deviation \(\Sigma \) leads to the description of the long-term creep mechanisms.

As mentioned above, the stress dependence of the attempt rate \(\gamma _{T}\) essentially means that the effect of the imposed stress modifies the height of the dynamic barrier, i.e., accelerates or slows down the molecular rearrangements. Therefore, by the above analysis, three main factors, namely the instantaneous elastic response and the magnitude and distribution of the retardation times, are taken into account. In addition, the effect of the imposed stress on all these factors is to be investigated.

The main concept of this hypothesis lies in the following assumption: when a creep experiment is performed and designed to last a certain period of time, it is a matter of question whether the imposed stress will be able to highlight all the characteristic areas of creep, namely primary, secondary, and tertiary one. Consequently, when the creep stress level changes, the range of the potential dams that are dominantly involved in the evolution of the phenomenon changes also. This does not mean, of course, that the areas of the material that have been left out of the spectrum do not follow retardation mechanisms, but their contribution to the available time domain carried out by the experiment is not significant. In other words, areas with very long retardation times will take part if we have an adequate time domain to highlight the tertiary area of creep, and areas with very short retardation times contribute to the initial instantaneous recording of deformation, and their contribution is incorporated into the instantaneous elasticity of the material. In the following paragraphs, to validate the model’s capability, three sets of creep experiments taken from the literature will be analyzed. Various polymeric structures exhibiting different features of nonlinear viscoelasticity are examined, and the model was proved to adequately describe this behavior.

3 Model validation: Results and discussion

3.1 Creep results of 90° carbon-epoxy composite

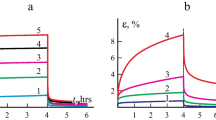
The creep strain experimental results of a 90° carbon-epoxy composite taken from the work by Zaoutsos and Papanicolaou (2010) were analyzed with our model. Five stress levels, fractions of the ultimate tensile strength (equal to 65 MPa), namely 30%, 40%, 50%, 60%, and 70%, were examined. More specifically, stress levels equal to 19.5, 26, 32.5, 39, and 45.5 MPa were studied. Creep testing was performed at ambient temperature, and the time period was 168 hrs. The experimental results of creep strain are illustrated in Fig. 1. On the basis of these results, the creep compliances were hereafter plotted and shown in Fig. 2.

Fig. 1
figure 1

Creep strain of 90° carbon-epoxy composite at various stresses. Points: Experimental results after Zaoutsos and Papanicolaou (2010). Lines: Model simulation

Full size image
Fig. 2
figure 2

Model simulation of the creep compliance curves of 90° carbon-epoxy composite at various stresses on the basis of the data of Fig. 1

Full size image

From this plot, the nonlinear viscoelasticity is obvious since the compliances do not overlap each other. On the basis of the constitutive equation (Eq. (3)), the creep strain \(\varepsilon (t)\) for uniaxial creep under a constant stress \(\sigma _{0}\) is given by

$$ \varepsilon (t) = \frac{\sigma _{0}}{\mu _{0}} + \int _{0}^{t} R(t - \tau )\varepsilon (\tau ) d\tau , $$
(11)

where \(R(t)\) is given by

$$ R(t,u) = \int _{0}^{t} \Gamma (u) \exp \left [ - \Gamma (u) (t - \tau ) \right ] \varepsilon (\tau ) d\tau , $$
(12)

where \(t\) is the time and \(\tau \) the prior time.

In our analysis, the elastic stiffness \(\mu _{0}\) is considered to be constant at every specific temperature examined. This is a reasonable consideration, however it is not adopted for a number of works where the elastic stiffness varies with stress and includes an additional parameter. The numerical implementation was performed following the subsequent procedure. Starting from the experimental results of the lower stress equal to 0.3 of the ultimate tensile strength of the material and combining Eqs. (11) and (12), the calculation of the involved parameters could be performed. The necessary parameters are the elastic stiffness \(\mu _{0}\), the mean value \(V\), and the standard deviation \(\Sigma \) of the distribution function \(p(u)\) according to Eq. (9), as well as parameter \(\gamma _{T}(\sigma )\). The model parameters were evaluated for the best approximation of the creep strain results by a back analysis procedure.

As soon as the creep strain at the first stress level was simulated, it was postulated that the creep strain at the subsequent stresses could be calculated almost with the same parameters of the distribution function by estimating the different value of \(\gamma _{T}(\sigma )\), performing a back analysis procedure. Finally, the parameter values were checked again for all stress levels to ensure their uniqueness. Hereafter, the validity of Eq. (8), which assumes a linear trend of the logarithmic value of \(\gamma _{T}(\sigma )\) with varying stress, was validated.

The model parameter values for the 90° carbon-epoxy composite are presented in Table 1. The mean value \(V\) was taken equal to zero in all cases.

Table 1 Model parameter values for the creep results of 90° carbon-epoxy composite (Zaoutsos, Papanicolaou, 2010)
Full size table

An important issue in our procedure is the convergence of the numerical calculations.

To solve the nonlinear integral equation (Eq. (11)), we have followed the method of finite differences with initial conditions the elastic strain \(\varepsilon (0)=\sigma _{0}/\mu _{0}\) and \(d\varepsilon (0)=0\).

Performing numerical calculations within the frame of Mathematica, every specific time \(t\) was divided into a finite number of micro differences \(\Delta t\), and utilizing Eq. (11), the strain could be evaluated as the algebraic sum of finite infinitely small quantities.

Therefore, creep strain \(\varepsilon (t)\) is numerically solved according to the following reduction formula:

$$ \varepsilon [m + 1] = \frac{\sigma _{0}}{\mu _{0}} + \mathrm{Sum}\left [ R(m - j) \varepsilon (j) \Delta t,\{ j,0,m,1\} \right ]. $$
(13)

Given that the method of small time steps requires a very high computational time, function \(R(t)\) was calculated at every time step by the following differential equation:

$$ \frac{dR(t,u)}{dt} = \Gamma (t,u) \left [ \varepsilon (t) - R(t,u) \right ] $$
(14)

with the initial condition

$$ R(0,u)=0. $$
(15)

Hereafter, the calculated function \(R(t)\) is introduced in Eq. (13). The problem that arises here is the selection of the infinitesimal difference \(\Delta t\) that can ensure a convergence in our solution. Consequently, this value of \(\Delta t\) should be lower than the lower retardation time included in the specific experimental data under consideration. Therefore, taking into account Eq. (4) and the fact that \(\Gamma (u)\) (or the quantity \(\gamma _{T}(\sigma )\)) attains the physical meaning of the inverse retardation time, the \(\Delta t\) value should satisfy the following condition:

$$ \Delta t < \exp [ - \gamma _{T}(\sigma )]. $$
(16)

The selection of \(\Delta t\) by this procedure could lead to a high convergence in our solution, in spite of the very long computing time required for this analysis. In this way, the primary and secondary creep stages could be adequately modeled.

On the basis of Eq. (8), the stress variation of parameter \(\ln[\gamma _{T}(\sigma )]\) is illustrated in Fig. 3, indicating a linear trend with known slope \(\beta \) and intersection A. Actually, Eq. (5) takes the form \(\ln \gamma _{T}(\sigma ) = - 14 + 0.1538 \sigma \) for the case of 90° carbon epoxy material.

Fig. 3
figure 3

Variation of parameter \(\gamma _{T}\)(\(\sigma \)) with stress for 90° carbon-epoxy composite

Full size image

The simulated creep strain and compliance curves are illustrated in comparison with the experimental results in Figs. 1 and 2. It is obvious from these curves that the model is capable of describing the nonlinear creep strain results in a variety of stresses.

4 Creep results of PA66

The creep experimental results of a typical polyamide PA66 taken from Yang et al. (Part II, 2006) were performed at 23, 50, and 80 °C, at three stresses equal to 20, 30, and 40 MPa for a time period of 200 hrs, including the primary and secondary creep stage.

The experimental results are illustrated in Fig. 4. The stress levels are below 80% of the ultimate tensile strength of PA66, as it is mentioned by Yang et al. (Part II, 2006b), and the creep time examined includes the primary and secondary creep stage.

Fig. 4
figure 4

Creep strain results of PA66 at various stresses and temperatures. Points: Experiment (Yang et al. 2006a, 2006b). Lines: Model simulation

Full size image

Following these results, a nonlinear viscoelastic response is revealed, and the onset of nonlinearity takes place at about 20 MPa at all temperatures examined. As it was also mentioned by Yang et al. (Part II, 2006b), from the isochrones curves, the nonlinearity starts beyond the stress of 20 MPa at all temperatures investigated. Performing a similar calculation procedure, as shown in the previous paragraph, the creep strain experimental data at all temperatures were simulated with a very good accuracy, which is shown in Fig. 4, whereas the variation of the \(\gamma _{T}\)(\(\sigma \)) function is depicted in Fig. 5.

Fig. 5
figure 5

Variation of parameter \(\gamma _{T}\)(\(\sigma \)) with stress at three different temperatures

Full size image

For temperatures 50 and 80 °C, the stress variation of parameter ln[\(\gamma _{T}\)(\(\sigma \))] is again confirmed, which is illustrated in Figs. 5b, 5c, indicating a linear trend with known slope and intersection. The form of Eq. (5) is \(\ln \gamma _{T}(\sigma ) = - 13.16 + 0.55 \sigma \) for 50 °C, while it is \(\ln \gamma _{T}(\sigma ) = - 16.33 + 0.85 \sigma \) for 80 °C. Parameter A and \(\beta \) values are shown in Table 2.

Table 2 Model parameter values for the creep results of PA66 (Yang et al., Part II, 2006b)
Full size table

As it is shown in Fig. 5 for 23 °C, for stresses equal to 15 and 20 MPa, the creep response is almost linear with no strong stress dependence. The slope is higher for stresses 30 and 40 MPa. Therefore, different values of parameter \(\gamma _{T}\)(\(\sigma \)) on the basis of the two different slopes were employed for the simulation of the creep results at 23 °C. The corresponding equations are:

$$\ln \gamma _{T}(\sigma ) = - 9.25 + 0.05 \sigma $$

and

$$ \ln \gamma _{T}(\sigma ) = - 24.25 + 0.55 \sigma . $$

Correspondingly, for the first and second slope, the resulting values of parameters A and \(\beta \) are shown in Table 2.

It is therefore obtained that the employed analysis was proved to model adequately the nonlinear viscoelastic response of the PA66 material examined.

Regarding a very interesting issue of the long-term creep strain prediction, the model was proved to be capable of predicting it. Referring to the results by Yang et al. (Part II, 2006b), the master curve of the creep compliance at 15 MPa at a reference temperature 23 °C was constructed by applying the time-temperature superposition principle. This plot is illustrated in Fig. 6, revealing the long-term creep response of PA66 studied.

Fig. 6
figure 6

Long-term creep compliance curve at 15 MPa and 23 °C for PA66. Points: Experimental results after Yang et al. (2006a, 2006b). Line: Model simulation

Full size image

Performing calculations with the same set of parameters at 23 °C and employing the parameter A and \(\beta \) values (the first set of Table 2 at 23 °C), the long-term creep response could also be captured and depicted in Fig. 6. Additionally, the long-term creep strain of PA66 at 23 °C for 30 MPa for 340 hrs was analyzed. In Fig. 7 the experimental results after Yang et al. (Part II, 2006b) are plotted together with the model simulation. Therefore, the present analysis succeeds in predicting the long-term creep response, utilizing the parameter values of the short-term creep time.

Fig. 7
figure 7

Long-term creep strain curve for PA66 at 30 MPa and 23 °C. Points: Experimental results after Yang et al. (2006a, 2006b). Line: Model simulation

Full size image

5 Creep results of a carbon black reinforced elastomer

Gacem et al. (2008) conducted creep experiments on a synthetic carbon black filled elastomer. This material is used in manufacturing traditional multilayer plate incorporating metallic and visco-elastic materials for machine suspension. In addition, this composite structure is used in brake system for vibro-acoustic isolation. Therefore, the visco-elastic material is worked as a damping layer (Gacem et al. 2008). Creep testing at room temperature at stress levels equal to 0.5, 1.0, 1.5, 2.0, and 2.5 MPa were conducted for a wide time range. The experimental data are shown in Fig. 8.

Fig. 8
figure 8

Creep strain of reinforced elastomer at various stresses. Points: Experimental results after Gacem et al. (2008). Lines: Model simulation

Full size image

The corresponding creep compliances are shown Fig. 9 for the three stress levels for a time period of seven days, while for the stress of 2.5 MPa, the compliance in a wider time region (115 days) is produced.

Fig. 9
figure 9

Model simulation: Creep compliance curves of reinforced elastomer at various stresses on the basis of the experimental results of Fig. 8. Points: Experimental results after Gacem et al. (2008)

Full size image

What is important to be mentioned here is that the compliance curves are in the opposite order than that of the creep strain curves. It is not the case for a high number of creep results performed in various research works, which reveals a different aspect of nonlinear viscoelasticity. Considering this behavior and given that the creep compliance actually reflects the creep strain per unit stress, in the case of the elastomer, the stress increment incommodes the creep strain evolution.

It will be shown in the following that the proposed model will be able to capture this trend. Performing analogous calculations, as already mentioned, the model simulations of creep strain and creep compliances are illustrated in comparison with experimental data in Figs. 8 and 9. The model parameter values are shown in Table 3. It is obvious that the model succeeds to predict the experimental long-term creep compliance curve with the model parameters utilized in the creep curves of the other stress levels. Regarding parameter \(\gamma _{T}\)(\(\sigma \)), it is plotted for various stresses in Fig. 10.

Fig. 10
figure 10

Variation of parameter \(\gamma _{T}\)(\(\sigma \)) with stress for the reinforced elastomer

Full size image
Table 3 Model parameter values for the creep results of the carbon black reinforced elastomer (Gacem et al. 2008)
Full size table

The corresponding equation of its linear trend with stress is \(\ln \gamma _{T}(\sigma )=9-2 \sigma \), where \(\sigma \) is the stress. It is observed that this plot has a negative slope with increasing stress. The negative slope is associated with the higher creep resistance exhibited by the elastomeric material. The stress increment leads to a reduction of the space available for new molecular conformations. On the other hand, the positive slope, which was obtained for the materials analyzed in the previous paragraphs, can be related to the fact that stress facilitates the creep strain evolution.

It is obvious from the above presented analysis that the model is capable of describing the nonlinear creep strain results of various polymeric types at various stresses and temperatures. In addition, it was proved that the long-term creep can be predicted utilizing the same set of parameters as in the short-term creep tests. Moreover, it was possible to model the inversed ordering of the creep compliance curves in the case of the elastomeric material.

Within the frame of our analysis, it was shown that creep response can be modeled assuming that the imposed stress affects only the retardation times, and there is no need to change the elastic modulus of the materials, revealing a low number of required model parameters compared to well-established theoretical treatments.

6 Conclusion

The present work is an attempt to systematically describe the nonlinear viscoelastic behavior of polymers, as recorded in creep experiments of representative polymeric materials in the literature. The theoretical analysis is based on the theory introduced and further elaborated in the previous works and is expressed by a time-dependent constitutive equation having the form of a memory integral. One of the decisive points of this analysis is the distribution function type followed by the energy barriers, which need to be overcome for transitions of molecular junctions to occur. Two model parameters, namely the mean value and the standard deviation of the distribution function, are introduced and need to be calculated. In addition, the role of the imposed stress level in a creep experiment is further analyzed. It was shown that the stress level affects the retardation times of the material, which are related to the attempt rate \(\gamma \) of the molecular domains, determining the time evolution of the characteristic sizes. Contrary to the previous works, the effect of stress level on the elastic constant of the material is not accounted for. Therefore, the elastic stiffness is maintained constant at the various stress levels examined. Creep experimental results of various polymeric types taken from the literature were utilized for the model validation. Various aspects of the nonlinear viscoelastic response exhibited by the materials under investigation could be described. Namely, both the case where the stress increment enhances the creep strain evolution and the case where the stress increment accordingly delays the creep strain development were examined. Moreover, the model was proved to predict the long-term creep response on the basis of model parameter values estimated from the short-term creep experiments.